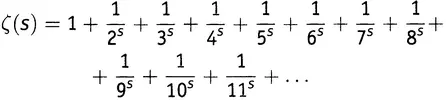Можно, конечно, и именно так и делается. Если пожелать возвести −4 + 7 i в степень 2 − 3 i , то надо сначала вычислить логарифм числа −4 + 7 i , который оказывается равным примерно 2,08719 + 2,08994 i . Затем надо умножить это на 2 − 3 i , что даст 10,4442 − 2,08169 i . И теперь возвести число e в эту степень, что и даст окончательный результат −16793,46 − 29959,40 i . Итак,
(−4 + 7 i ) 2 − 3 i = −16793,46 − 29959,40 i .
Ничего сложного! Еще пример: поскольку −1 = e πi , извлечение квадратного корня из обеих частей даст i = e πi /2. И если теперь возвести обе части в степень i , то, снова пользуясь 3-м правилом действий со степенями, получим i i = e −π /2. Заметим, что это вещественное число, равное 0,2078795763….
Поскольку можно возводить любое комплексное число в любую комплексную степень, несложным должно оказаться возведение вещественного числа в комплексную степень. Следовательно, для заданного комплексного числа z можно вычислить 2 z , 3 z , 4 z и т.д. Понятно, к чему идет дело. Можно ли расширить область определения дзета-функции
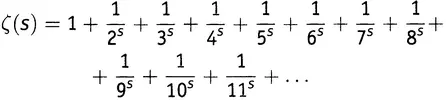
в мир комплексных чисел? Можно, конечно. С комплексными числами, доложу вам, можно делать что угодно.
III.
Поскольку формула для дзета-функции остается бесконечной суммой, возникает вопрос о сходимости. Оказывается, что сумма сходится для любого комплексного числа, вещественная часть которого больше единицы. Математики скажут «в полуплоскости Re( s ) > 1», где Re( s ) используется для обозначения вещественной части числа s .
Но, как и в случае с дзета-функцией вещественных аргументов, для расширения области определения в те области, где бесконечная сумма не сходится, можно применить некоторые математические уловки. В результате получается полная дзета-функция, область определения которой составляют все комплексные числа за единственным исключением числа s = 1. Там, как мы еще в самом начале убедились при помощи колоды карт (см. главу 1), у дзета-функции нет значения. Везде, кроме этой точки, она имеет единственным образом определенное значение. Имеются, конечно, и такие места, где это значение нулевое. Это мы и раньше знали. Графики из главы 9.iv показывают, что дзета-функция принимает равное нулю значение для всех отрицательных четных чисел −2, −4, −8, …. Мы на них не останавливаемся, потому что, как уже было замечено, они не слишком важны. Это тривиальные нули дзета-функции. Могло ли бы так случиться, что значение дзета-функции равно нулю при некоторых комплексных аргументах? И что, это и будут нетривиальные нули, упоминаемые в Гипотезе? Делайте ваши ставки; но я несколько забежал вперед в нашей истории.
IV.
Сорок лет назад блестящий, но эксцентричный Теодор Эстерман [112]написал учебник, озаглавленный «Комплексные числа и функции», в котором содержались всего два рисунка. «Я <���… > избежал всякого обращения к геометрической интуиции», — объявлял автор в предисловии. Известно некоторое число родственных ему душ, однако большая часть математиков не следует подходу Эстермана. Они трактуют теорию функций комплексной переменной в высшей степени визуально. Многие из нас полагают, что функции комплексной переменной легче освоить, пользуясь некоторыми наглядными образами.
Но как же можно наглядно представить себе функцию комплексной переменной? Возьмем простейшую нетривиальную функцию комплексной переменной — функцию возведения в квадрат. Есть ли какой-нибудь способ узнать, на что она похожа?
Скажем сразу: от обычных графиков толку здесь немного. В мире вещественных чисел можно изобразить функцию на графике таким образом: проводим прямую, изображающую аргументы (как мы помним, вещественные числа живут на прямой); затем проводим другую прямую под прямым углом к первой и используем ее для значений функции. Чтобы выразить тот факт, что данная функция превращает число x в число y , двигаемся на восток от нулевого аргумента на расстояние x (на запад, если x отрицательно), а затем на север от нулевого значения на расстояние y (на юг, если y отрицательно). Отмечаем там точку. Повторяем такое для стольких значений функции, сколько нам не лень вычислить. Это и дает график функции. На рисунке 13.1 приведен пример.
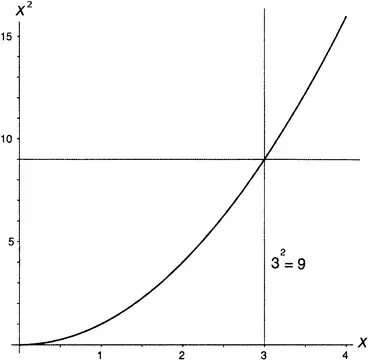
Рисунок 13.1.Функция x 2.
Читать дальше