Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

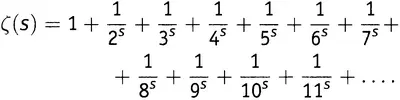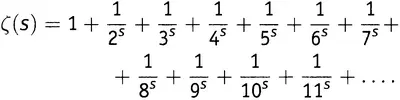
оказаться больше, чем просто «все числа, большие 1»?

Конечно может. Иначе зачем бы мы тут стали влезать во все эти подробности? Да, дзета-функция имеет значения при аргументах, меньших 1. На самом деле, как и функция 1/(1 − x ), она имеет значения при всех числах за единственным исключением x = 1.

Сейчас подходящий момент, чтобы привести график дзета-функции, который продемонстрировал бы все ее свойства в широком интервале значений. К сожалению, это невозможно. Как уже упоминалось, кроме как для простейших функций, обычно нет хорошего и надежного способа показать функцию во всем ее великолепии. Близкое знакомство с функцией требует времени, терпения и тщательного изучения. Можно, однако, изобразить дзета-функцию по кускам. На рисунках с 9.3 по 9.10 показаны значения ζ(s) для некоторых аргументов, находящихся слева от s = 1, хотя для этого потребовалось выбрать свой собственный масштаб на каждом графике. Понять, где мы находимся, можно, руководствуясь подписанными аргументами (на горизонтальной оси) и значениями (на вертикальной оси). При обозначении масштаба m указывает на миллион, tr на триллион, mtr обозначает миллион триллионов, a btr — миллиард триллионов.

Коротко говоря, когда s лишь немного меньше единицы (рисунок 9.3), значения функции очень большие по величине и отрицательные — как если бы при движении на запад при пересечении линии s = 1 значения внезапно переметнулись из бесконечности в минус бесконечность. Если продолжить путешествие по рисунку 9.3— т.е. устремлять s ближе и ближе к нулю, — то подъем вверх радикально замедляется. Когда s равно нулю, ζ(s) равна − 1/ 2. При s = −2 кривая пересекает ось s , т.е. ζ(s) равна нулю.

Рисунок 9.3.

Затем (мы по-прежнему двигаемся на запад, добравшись теперь до рисунка 9.4) график взбирается на относительно скромную высоту (в действительности до 0,009159890…), а после этого поворачивает вниз и снова пересекает ось при s = −4. График попадает в неглубокую впадину (−0,003986441…), а после нее снова взбирается вверх и пересекает ось при s = −6. Еще один невысокий пик (0,004194…), спуск до пересечения с осью при s = −8 и далее в несколько более глубокую впадину (−0,007850880…), затем пересечение с осью в точке −10, после чего уже довольно заметный пик (0,022730748…), пересечение с осью при s = −12, впадина поглубже (−0,093717308…), пересечение с осью при s = −14 и т.д.

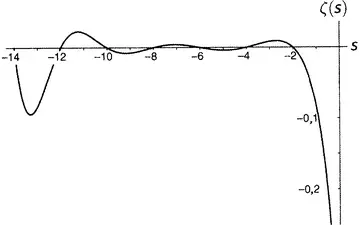
Рисунок 9.4.

Дзета-функция равна нулю при каждом отрицательном четном числе, а по мере продвижения на восток (рисунки от 9.5 до 9.10) последовательные пики и впадины быстро делаются все более и более значительными. Последняя показанная впадина расположена при s = −49.587622654 … , а глубина ее составляет около 305 507 128 402 512 980 000 000. Сами видите, как нелегко изобразить дзета-функцию на одном графике.

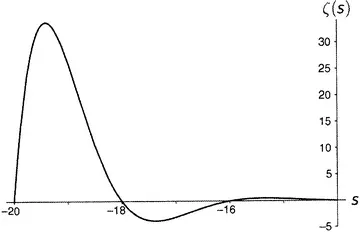
Рисунок 9.5.

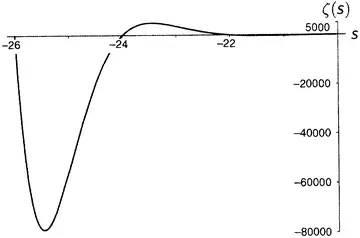
Рисунок 9.6.

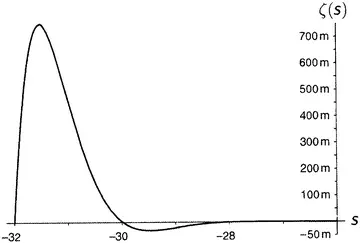
Рисунок 9.7.

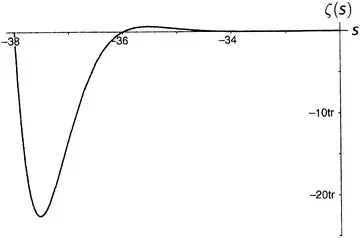
Рисунок 9.8.

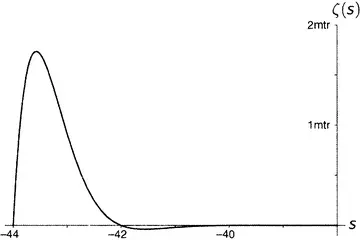
Рисунок 9.9.

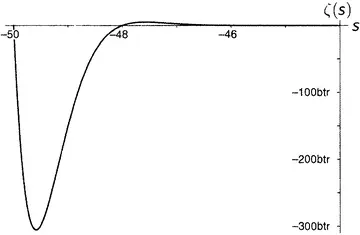
Рисунок 9.10.

Ho как я получил все эти значения ζ(s) для s , меньших 1? Мы уже видели, что бесконечный ряд из выражения (9.1)для этого непригоден. А что пригодно ? Если бы ради спасения своей жизни мне пришлось вычислить значение ζ (−7,5), как бы я к этому подступился?

Я не могу объяснить этого в полной мере, потому что такое объяснение требует слишком значительного погружения в математический анализ. Но я попробую передать общую идею. Сначала определим некоторую новую функцию, используя бесконечный ряд, слегка отличный от ряда в выражении (9.1). Это η- функция; η (читается «эта») — седьмая буква греческого алфавита. Определим η- функцию как