Без примесей, чистокровный (франц.). (Примеч. перев.)
Гипотеза Римана эквивалентна, в частности, ряду утверждений о делителях натуральных чисел, например, такому утверждению: «Для всякого натурального числа n ≥ 5041 сумма его делителей меньше величины e γn ln(ln n )». Здесь γ — упоминавшееся число Эйлера-Маскерони, в России чаще называемое просто постоянной Эйлера . (Примеч. перев.)
Цепь событий в наикратчайшем изложении такова. Метод, принятый в Principia Mathematica, не давал гарантии от ошибок, подобных той, на которую Рассел обратил внимание в работе Фреге. Программа «метаматематики» Гильберта ставила целью объять и логику, и математику в единый четкий формализм. Это послужило мотивировкой исследований Курта Геделя и Алана Тьюринга. Гедель доказал ряд важных теорем путем построения соответствия между символами типа гильбертовых и числами; Тьюринг закодировал и инструкции, и данные в виде чисел в своей идее «машины Тьюринга». Ухватившись за эту идею, Джон фон Нейман развил концепцию хранящейся в памяти программы — концепцию, на которой основано все современное программное обеспечение и согласно которой и код, и данные можно единообразно представить в памяти компьютера…
В письме к брату от 26 июня 1854 г. он упоминает возобновление mein altes Übel — «моей старой болезни», вызванное разыгравшейся непогодой.
Ныне — в муниципалитете Вербания.
Weender Chaussee было позднее переименовано в Bertheaustrasse .
В оригинале песню Тома Апостола «Где же нули у функции дзета» можно послушать (и даже посмотреть видеоклип с исполнением первого куплета) по адресу:
http://olimu.com/Riemann/Song.htm. (Примеч. перев.)
Вилликенс и его Дина. (Примеч. перев.)
В Англии, как правило, в регби играют в частных школах (а в футбол — в остальных). (Примеч. перев.)
«0 святой отец, прими мою исповедь. Я оставил одну бедную девочку в чертовски трудном положении». (Примеч. перев.)
Поскольку в данном случае — при движении вверх по критической прямой — t, очевидно, положительно, указание на его модуль излишне, если только оно не служит попаданию в размер стиха. (Примеч. перев.)
Упомянутые в главе 8.ii условия Коши-Римана, которые определяют «хорошо ведущие себя функции», как раз выделяют такие функции, для которых зависимость от контура, по которому ведется интегрирование между двумя заданными точками на комплексной плоскости, носит контролируемый, «дискретный» характер. (Примеч. перев.)
Или, правильней:
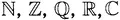
и так далее.
В оригинале 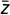 .
.
В оригинале обозначается как 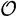 .
.
В оригинале обозначается как 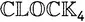 .
.
Джон Дербишир
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Главный редактор Варвара Горностаева
Художник Андрей Бондаренко
Ведущий редактор Галина Юзефович
Ответственный за выпуск Мария Косова
Технический редактор Татьяна Тимошина
Корректор Екатерина Комарова
Верстка Марина Харитонова
ООО «Издательство Астрель»,
обладатель товарного знака «Издательство Corpus»
129085, г. Москва, пр-д Ольминского, 3а
Подписано в печать 11.01.2010. Формат 60x90/16
Бумага офсетная. Гарнитура «MetaNormalC»
Печать офсетная. Усл. печ. л. 29
Тираж 5000 экз. Заказ № 0808.
Общероссийский классификатор продукции OK-005-93, том 2;
953000 — книги, брошюры
Санитарно-эпидемиологическое заключение
№77.99.60.953.Д.012280.10.09 от 20.10.2009
Охраняется законом РФ об авторском праве. Воспроизведение всей книги или любой ее части воспрещается без письменного разрешения издателя. Любые попытки нарушения закона будут преследоваться в судебном порядке.
Отпечатано в соответствии с предоставленными материалами в ЗАО «ИПК Парето-Принт»
г. Тверь, www.pareto-print.ru
Издание осуществлено при техническом содействии ООО «Издательство ACT», ООО «Издательство Астрель»
Читать дальше

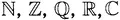
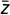 .
.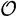 .
.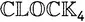 .
.










