По мере прибавления новых членов сами они убывают, а положительные и отрицательные до некоторой степени сокращают друг друга при суммировании, так что мы зарабатываем сходимость. Эта сходимость, правда, страшно медленная. Для получения результата с точностью в три значащие цифры приходится складывать более 7000 членов; в четыре цифры — более 86 000. На графике на рисунке 21.6 показаны первые 1000 результатов (хотя некоторые из самых левых при выбранном масштабе оказались за пределами рисунка); на этот раз не делается никаких попыток соединить точки между собой. Видно, что члены под знаком суммы действительно уменьшаются, хотя и делают это с достаточной ленцой.
Рисунок 21.6.То же, что на рисунке 21.5, но показана 1000 значений (точки не соединены между собой).
Окончательный результат равен −0,370816425…. Это, как мы помним, второй член в выражении (21.1). Первый же член — это в нашем случае Li(20), равный 9,90529997763…. Третий равен ln 2, что составляет 0,69314718055994…. И четвертый член, тот самый надоедливый интеграл, добавляет пустячный результат 0,000364111…. Подставим все это в выражение (21.1)и — хлоп! — J (20) = 9,58333333… (что мы, конечно, и так знали).
VIII.
Закончим тем, что с использованием формулы Римана проведем полное вычисление π (1000 000) — т.е. числа простых чисел в пределах одного миллиона — не ради веселья, хотя веселье и немалое, а для того, чтобы сделать несколько важных замечаний по поводу остаточного члена.
Как мы помним из главы 19.iv,
π (1000 000) = J (1000 000) − 1/ 2 J (√1000 000) − 1/ 3 J ( 3√1000 000) − ….
Сколько же членов в правой части надо вычислять? До тех пор пока числа в скобках не станут меньше 2, потому что J(x) равна нулю, когда x меньше 2. Корень девятнадцатой степени из 1000 000 равен 2,069138…, а корень двадцатой степени 1,995262… Следовательно, можно остановиться на 19. Поскольку число 19 свободно от квадратов и имеет только один простой делитель — самого себя, — функция Мебиуса μ (19) имеет значение −1. Таким образом, последний член в правой части равен − 1/ 19 J ( 19√1000 000). Всего в правой части будет 13 слагаемых, поскольку между 1 и 19 функция Мебиуса принимает ненулевые значения 13 раз — при аргументах 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19. Напомним, что функция Мебиуса равна нулю всякий раз, когда аргумент делится на точный квадрат (например, 4 или 9).
Каждое из этих 13 слагаемых состоит из четырех членов: главный член, вторичный член (куда и входят нули дзета-функции), член с ln 2 и интегральный член. Если сложить все эти 52 куска, получится π (1000 000) — число, про которое мы заранее знаем из главы 3.iii, что оно равно 78 498.
Вся эта арифметика расписана в таблице 21.1 (там опущены строки с N , для которых J(N) равно нулю). Двигаясь вдоль строки N и используя y для обозначения N- го корня из одного миллиона, имеем главный член 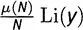 , вторичный член
, вторичный член 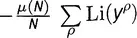 , член с ln 2, равный
, член с ln 2, равный 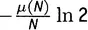 , и интегральный член
, и интегральный член 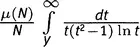 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
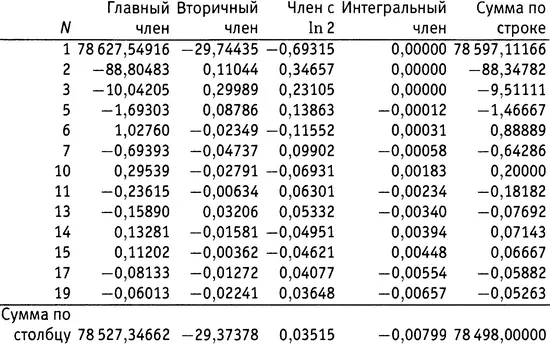
Таблица 21.1.Вычисление π (1000 000).
В качестве простой проверки возьмем строку с N = 6. Поскольку миллион — это 10 6, корень шестой степени из миллиона — это просто 10. Значение J (10) легко посчитать — оно оказывается равным 16/ 3. Поскольку число 10 свободно от квадратов и представляет собой произведение двух простых чисел, функция Мебиуса μ (10) имеет значение +1. Итак, в строке с N = 6 последний столбец должен быть равен (+1)×( 1/ 6)×( 16/ 3). Это составляет 8/ 9, что и говорится в суммарной колонке для строки с N = 6.
При N = 1 главный член, равен просто Li(1000 000); именно такое приближение к точному ответу дает нам ТРПЧ. Какова же разница между этим приближением и π (1000 000)? Ответ получается мгновенно путем простого вычитания: разность, вычисленная как π (1000 000) минус Li(1000 000) (чтобы сохранить знаки в нашей таблице), равна −129,54916. Из чего эта разница слагается?
Читать дальше

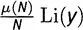 , вторичный член
, вторичный член 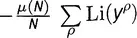 , член с ln 2, равный
, член с ln 2, равный 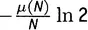 , и интегральный член
, и интегральный член 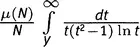 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).











