Генри Дьюдени - Пятьсот двадцать головоломок

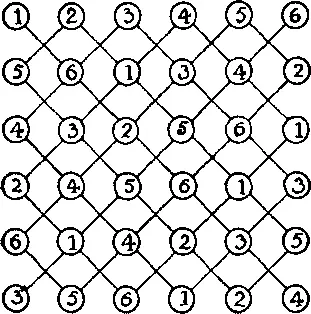
— Вам, должно быть, известно, — сказал незнакомец, — выражение «Сакраменто — край богатый, золото гребут лопатой». Так вот, на одном участке земли размечено 36 кругов, в каждом из кругов стоит мешок, содержащий столько долларов, сколько указано на схеме. Разрешается брать любое число мешков, лишь бы не проходить дважды по одной и той же прямой.

Какую наибольшую сумму можно собрать?

456. Семеро детей.Четыре мальчика и три девочки садятся случайным образом в один ряд.

Какова вероятность того, что два ребенка на концах ряда окажутся девочками?

457. Крестики-нолики.В эту старинную игру умеет играть каждый ребенок. Квадрат расчерчивают на 9 клеточек. Каждый игрок по очереди ставит в свободную клеточку свой знак (крестик или нолик), стараясь выстроить три своих знака по одной прямой. Тот, кто сумеет добиться этого, выигрывает. Если играют два хороших игрока, то каждая партия у них неизменно должна оканчиваться вничью, поскольку никто из них не сможет выиграть (если только его соперник не допустит случайный промах).

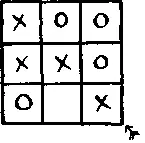
Можете ли вы доказать это утверждение? Можете ли вы быть уверены, что не проиграете встречу с самым лучшим игроком?

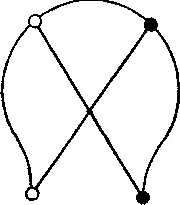
458. Игра в подкову.Вот небольшая игра под стать крестикам-ноликам. В нее играют двое. У одного игрока имеются две белые фишки, у другого — две черные. Играя по очереди, каждый из игроков ставит фишку на свободный кружок (см. рисунок), где она и остается. Когда все фишки расставлены, игроки могут их только передвигать вдоль линий от точки к точке, а проигрывает тот из них, чьим фишкам некуда ходить. На нашем рисунке играющий черными только что поставил свою фишку вниз. Теперь играющий белыми передвигает свою нижнюю фишку в центр и выигрывает. Черным следовало бы поставить свою вторую фишку в центр и добиться тем самым победы.

Какой из игроков должен победить в этой игре?

459. Перевертывание кости.Для этой игры нужна одна игральная кость. Первый игрок называет любое число от 1 до 6, а второй бросает кость. Затем они по очереди перевертывают кость в любую сторону, но не больше, чем на четверть полного оборота за один раз. К числу очков, названному первым игроком, прибавляется число очков, выпавших на верхней грани после бросания кости и каждого ее поворота. Выигрывает тот из игроков, которому удается при очередном повороте достичь суммы 25 очков или вынудить противника при следующем повороте превзойти 25 очков.

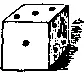
Приведу примерную партию. Игрок А называет 6, а игрок В , подбросив кость, получает 3 очка (как на рисунке), после чего сумма очков становится равной 9. Затем A повертывает кость вверх гранью с 1 очком, сумма становится равной 10 очкам, игрок В повертывает кость вверх гранью с 3 очками (сумма равна 13 очкам). Игрок А повертывает кость вверх гранью с 6 очками (сумма очков 19). Игрок В повертывает кость с 3 очками (сумма очков 22). Игрок А повертывает кость вверх гранью с 1 очком (сумма очков 23). Наконец, игрок В переворачивает кость вверх гранью с 2 очками, достигает суммы 25 очков и выигрывает.

Какое число должен назвать А , чтобы выиграть с наибольшими шансами? Помните, что числа на противоположных гранях кости всегда дают в сумме 7, то есть расположены парами 1—6, 2—5, 3—4.

460. Три кости.Мэйсон и Джексон играли в кости. У них было три кости, и выигрывал тот игрок, у которого сумма выпавших очков равнялась одному из двух чисел, названных им перед началом игры. Мэйсон назвал 7 и 13, и один из его удачных бросков показан на рисунке.

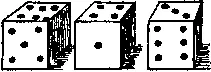
Каковы шансы Мэйсона на выигрыш при очередном бросании? Какие два числа должен назвать Джексон, чтобы шансы игроков на успех сравнялись?

461. Игра в 37.Вот красивая игра-головоломка, которая проста и в то же время чрезвычайно увлекательна. Большинству из вас может показаться, что у обоих игроков равные шансы на выигрыш и кто победит — дело случая. Однако в этой игре есть одна тонкость, зная которую, можно выигрывать с уверенностью.