Генри Дьюдени - Пятьсот двадцать головоломок

Я приведу в сжатой форме мое собственное доказательство, которое некоторые математики считают вполне приемлемым. Однако кое-кто полагает, что в нем имеются «пробелы». Доказательство дается в такой форме, которую может понять каждый. Однако следует помнить, что одно дело быть убежденным в чем-то, и совсем другое — дать этому строгое доказательство.

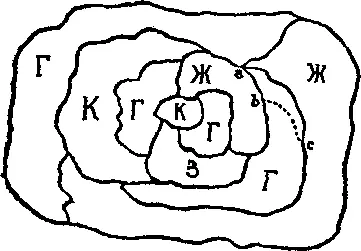
432. Раскрашивание карты.Однажды утром полковник Крэкхэм попросил своего юного сына раскрасить все 26 районов карты, изображенной на рисунке, так, чтобы любые два прилегающих друг к другу района имели разные цвета. Молодой человек с минуту смотрел на карту, а затем сказал:

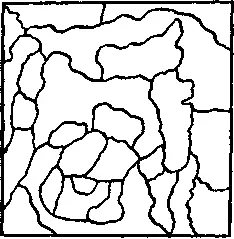
— В моем ящике не хватит одной краски.

Оказалось, что он прав. Сколько у него было красок? Пользоваться черной и белой красками ему не разрешалось.

433. Подаренные картины.У богатого коллекционера было 10 ценных картин. Ему захотелось сделать одному музею подарок, но коллекционер никак не мог сообразить, сколькими вариантами подарка он располагает: ведь подарить можно любую одну картину, любые две, любые три картины и т. д., можно даже подарить все десять картин.

Читатель, быть может, думает, что для ответа на этот вопрос потребуется долгий и утомительный подсчет; однако я приведу одно небольшое правило, позволяющее дать ответ во всех подобных случаях безо всяких трудностей и неблагодарной работы.

434. Выборы в парламент.Сколько существует разных способов, которыми можно избрать 615 членов парламента если имеются всего четыре партии: консерваторов, либералов, социалистическая партия и партия независимых? Мандаты могут распределяться, например, так: консерваторы — 310, либералы — 152, социалисты — 150, независимые — 3. Возможны и другие варианты: консерваторы — 0, либералы — 0, социалисты — 0, независимые — 615 или консерваторы — 205, либералы — 205, социалисты — 205, независимые — 0 и т. д. Кандидатов от каждой партии мы не различаем, поскольку для нас важно только общее количество кандидатов.

435. Скамья магистрата.Один мой приятель из Сингапура попросил меня некоторое время назад решить следующую задачу. На скамье одного магистрата (где именно, неизвестно) занимают места два англичанина, два шотландца, два уэльсца, один француз, один итальянец, один испанец и один американец. Англичане не хотят сидеть рядом, шотландцы не хотят сидеть рядом и уэльсцы тоже не желают сидеть рядом друг с другом.

Сколькими различными способами могут разместиться на скамье эти 10 человек так, чтобы никакие два человека одной и той же национальности не сидели рядом?

436. Переправа.Шесть родственников должны переправиться через реку в небольшой лодке, вмещающей одновременно только двоих. Мистер Вебстер, руководивший переправой, поссорился со своим тестем и сыном, кроме того, как ни прискорбно, но я должен заметить, что миссис Вебстер не разговаривает со своими матерью и невесткой. Отношения между ними столь натянуты, что не безопасно позволить враждующим сторонам вместе переправляться или вместе оставаться на одном и том же берегу реки. Кроме того, дабы предотвратить дальнейшие разногласия, ни одного мужчину нельзя оставлять с двумя женщинами или двух мужчин с тремя женщинами.

Как почтенному семейству перебраться на противоположный берег за возможно меньшее число рейсов? Никаких уловок вроде использования веревки или переправы на другой берег вплавь не допускается.

437. Миссионеры и каннибалы.Существует один необычный рассказ о трех миссионерах и трех каннибалах, которые должны были переправиться через реку в небольшой лодке, вмещающей одновременно только двух человек. Будучи наслышаны о вкусах каннибалов, миссионеры не могли позволить себе роскошь остаться на каком-нибудь берегу реки в меньшинстве. Только один из миссионеров и один из каннибалов умели грести.

Каким образом им удалось переправиться?

438. Бегство через реку.Во время бегства турецких войск при Трейсе небольшой отряд оказался на берегу широкой и глубокой реки. Здесь обнаружили лодку, в которой катались два мальчика. Лодка была такой маленькой, что могла выдержать только двоих детей или одного взрослого.

Каким образом офицер сумел переправиться вместе со своими 357 солдатами через реку, вернув в конце переправы лодку мальчикам? Сколько раз пришлось лодке проплыть от берега до берега?