Генри Дьюдени - Пятьсот двадцать головоломок

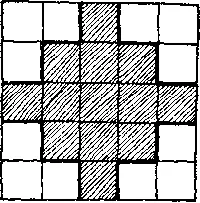
Можно ли построить магический квадрат, у которого суммы чисел, стоящих в любой строке, в любом столбце и на каждой из двух больших диагоналей, были бы одинаковы, из чисел от 1 до 25 включительно, если размещать в заштрихованных клетках только нечетные числа, а в остальных четные? Существует достаточно много решений этой задачи. Не смогли бы вы найти хотя бы одно из них?

383. Пятиконечная звезда.Головоломки со звездами обладают своеобразной притягательной силой. Я приведу пример такой головоломки с простой пятиконечной звездой.

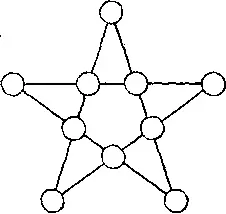
В каждый кружок изображенной здесь пятиконечной звезды требуется поместить различные числа таким образом, чтобы сумма любых четырех чисел, стоящих на одной прямой, равнялась 24. Решения с десятью последовательными числами не существует, однако вы можете использовать любые целые числа, какие пожелаете.

384. Шестиконечная звезда.В предыдущей задаче мы рассмотрели случай с пятиконечной звездой. Оказывается, с шестиконечной звездой дело обстоит еще интересней. В этом случае (см. рисунок) мы всегда можем использовать 12 последовательных чисел, от 1 до 12, а сумма четырех чисел на каждой прямой всегда окажется равной 26. Сумма чисел, стоящих в шести вершинах, может равняться любому числу от 24 до 54 включительно, кроме 28 и 50. В нашем примере эта сумма равна 24. Если вместо каждого из чисел вы подставите разность между ним и 13, то получите другое решение, дополнительное к данному, с суммой вершин, равной 54 (78 минус 24). Две дополнительные суммы в совокупности всегда дают 78.

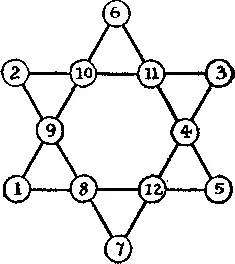
Я приведу общее число различных решений и укажу на некоторые любопытные законы, которым подчиняется эта задача, но ее решение предоставлю читателю. Существует 6 и только 6 размещений, при которых сумма чисел на каждой прямой и во всех вершинах равна 26. Можете ли вы найти одно из них или даже все?

385. Семиконечная звезда.Мы уже познакомились вкратце с пяти- и шестиконечными звездами. Случай с семиконечной звездой особенно интересен. Все, что от вас требуется, это разместить в кружочках числа от 1 до 14 так, чтобы в любых четырех кружочках, лежащих на одной прямой, они в сумме давали 30.

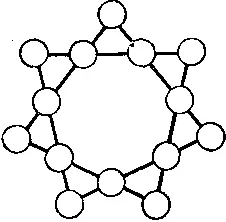
Если вы нарисуете диаграмму, подобную изображенной на нашем рисунке, и воспользуетесь перенумерованными фишками, то вам будет трудно не подпасть под очарование этой головоломки. Возможно, однако, что никто из читателей не натолкнется на простой способ ее решения и решение будет найдено лишь благодаря терпению и удаче. И все же, как и в подавляющем большинстве головоломок, уже встречавшихся на наших страницах, вы увидите, что и в данном случае решение подчиняется некоторому закону (если сумеете найти этот закон).

386. Две восьмиконечные звезды.Головоломки с пяти-, шести- и семиконечными звездами приводят нас к восьмиконечной звезде. Эту звезду можно образовать двумя различными способами (см. рисунок); здесь приводится и решение для первого варианта. Числа от 1 до 16 расположены таким образом, что сумма четырех из них вдоль каждой прямой равна 34. Если вместо каждого числа вы подставите разность между ним и 17, то получите дополнительное решение.

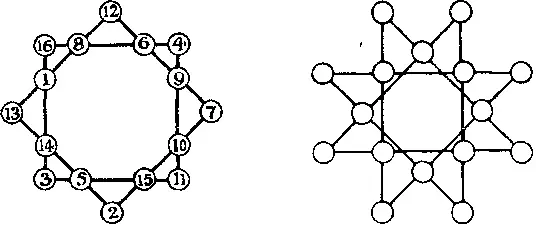
Если читатель попытается найти какое-нибудь решение для другой звезды, то, даже зная решение, приведенное выше, он убедится, что этот орешек расколоть не так-то просто. Однако я представлю вам головоломку в легкой и занимательной форме. Оказывается, что любое решение для первой звезды можно автоматически преобразовать в решение для второй, если правильно взяться за дело. Каждая прямая из четырех чисел в одном случае появится и в другом, изменится лишь порядок чисел. Располагая этими сведениями, вам нетрудно будет найти решение и для второй звезды.

387. Гарнизоны фортов.Перед вами на рисунке изображена система фортификационных сооружений. Всего имеется 10 связанных между собой фортов, цифры обозначают численность размещенных в них небольших гарнизонов. Командующий решил передислоцировать гарнизоны таким образом, чтобы вдоль каждой из пяти прямых размещалось по 100 человек.