Генри Дьюдени - Пятьсот двадцать головоломок

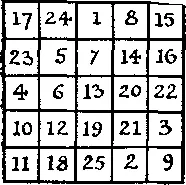
376. Недоразумение с магическим квадратом.Перед вами магический квадрат пятого порядка. Я обнаружил, что подавляющее большинство людей, не знакомых глубоко с теорией магических квадратов, убеждены, будто в квадратах пятого порядка в центре непременно должно стоять число 13. Один читатель, на протяжении многих лет забавлявшийся этим квадратом, был просто поражен, когда узнал от меня, что в центре такого квадрата может стоять любое число от 1 до 25.

Докажите, что это действительно так. Попытайтесь, например, составить магический квадрат пятого порядка, в центре которого стояла бы 1.

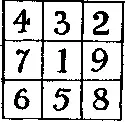
377. Разностные квадраты.Можете ли вы расположить 9 цифр в виде квадрата таким образом, чтобы в любой строке, в любом столбце и на каждой из больших диагоналей разности между суммой двух цифр и третьей цифрой совпадали между собой? На нашем рисунке приведен квадрат, в котором все строки и столбцы удовлетворяют требуемому условию — разность в них равна 3 (например, 4 + 2 - 3, 1 + 9 - 7, 6 + 5 - 8 и т. д.), а вот диагонали «подкачали», поскольку разности 8 - (4 + 1) и 6 - (1 + 2) получены запрещенным способом: не из одной цифры должна вычитаться сумма двух остальных, а из суммы двух — одна.

Сколько всего существует решений?

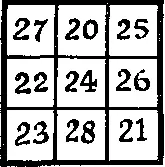
378. Так ли просто?Перед вами простой магический квадрат, у которого суммы чисел, стоящих в любой строке, в любом столбце и на главных диагоналях, равны 72. Головоломка состоит в том, чтобы превратить его в мультипликативный магический квадрат, у которого произведения чисел, стоящих в любой строке, в любом столбце или на любой из больших диагоналей, совпадали бы между собой. Не разрешается ни менять числа местами, ни прибавлять к ним что-либо, ни вообще пользоваться какими-либо арифметическими знаками! Можно лишь передвигать цифры внутри одной клетки. Так, вместо 27 разрешается брать 72.

Если вам удастся подобрать «ключ» к решению, то задача окажется необычайно простой. В противном случае решить головоломку почти невозможно.

379. Фокус с магическим квадратом.Этот фокус был весьма разрекламирован в США много лет назад.

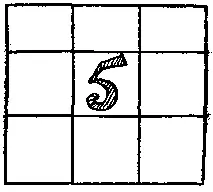
Заполните пустые квадраты (см. рисунок) цифрами (в каждом случае различными, чтобы никакие две клетки не содержали одинаковой цифры) так, чтобы сумма чисел, стоящих как можно в большем числе столбцов, строк и на диагоналях, равнялась 15. За разгадку «секрета» фокуса был назначен большой приз, но получить правильное решение не удалось никому.

Может быть, читатель разгадает, в чем здесь дело?

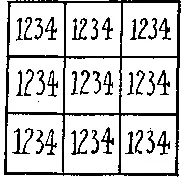
380. Магический квадрат из четырех цифр.Поскольку данный квадрат составлен из одного и того же числа 1234, естественно, что суммы чисел, стоящих во всех строках, столбцах и на диагоналях, равны между собой. Суть головоломки в том, чтобы составить и разместить 9 различных четырехзначных чисел (составленных из тех же самых четырех цифр) так, чтобы они тоже образовывали правильный магический квадрат. Помните, что все вместе числа должны содержать по девять экземпляров каждой из цифр 1, 2, 3, 4 и что это должны быть настоящие четырехзначные числа без каких-либо дробей; никакие трюки здесь не допускаются.

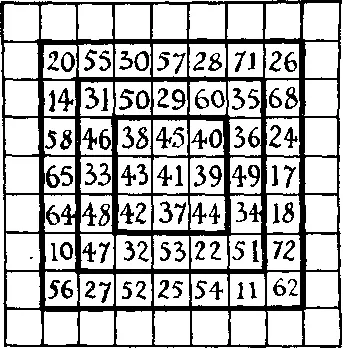
381. Прогрессирующие квадраты.Перед вами магический квадрат, постоянная которого, то есть сумма чисел в каждой строке, в каждом столбце и на каждой из двух диагоналей, равна 287. Если мы удалим числа, расположенные по краям, то останется другой магический квадрат, постоянная которого равна 205. Если мы опять удалим крайние числа, то получится квадрат с постоянной 123. Заполните теперь пустые клетки числами от 1 до 83 включительно так, чтобы получился магический квадрат с постоянной 369 на любой из 20 его прямых.

382. Условный магический квадрат.Хотя относительно простого построения магических квадратов добавить нечего, а по самому предмету существует весьма обширная, правда, разрозненная, литература, небольшие вариации с некоторыми новыми условиями всегда вызывают интерес. Вот один нетрудный пример.