97. Пятью девятками
Выразите число 10 пятью девятками. Укажите по крайней мере два способа.

Рис. 126
98. Десятью цифрами
Выразите 100, употребив все десять цифр. Сколькими способами можете вы это сделать? Существует не меньше четырех способов.
99. Четырьмя способами
Четырьмя различными способами выразите 100 пятью одинаковыми цифрами.
100. Четырьмя единицами
Какое самое большое число можете вы написать четырьмя единицами?
101. Загадочное деление
В следующем примере деления все цифры заменены звездочками, кроме четырех четверок. Поставьте вместо звездочек те цифры, которые были заменены.
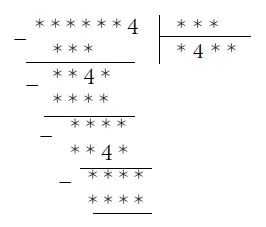
Задача эта имеет несколько различных решений.
102. Еще случай деления
Сделайте то же с другим примером, в котором уцелело только семь семерок:
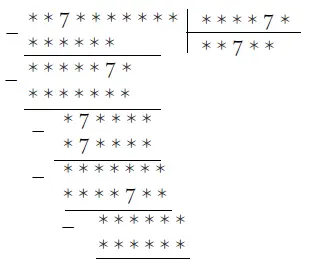
103. Что получится?
Сообразите в уме, на какую длину вытянется полоска, составленная из всех миллиметровых квадратиков одного квадратного метра, приложенных друг к другу вплотную.
104. В том же роде
Сообразите в уме, на сколько километров возвышался столб, составленный из всех миллиметровых кубиков одного кубометра, положенных один на другой.
105, Аэроплан
Аэроплан шириною 12 м был сфотографирован во время полета снизу, когда он пролетал отвесно над аппаратом. Глубина камеры 12 см.
На снимке ширина аэроплана равна 8 мм. На какой высоте летел аэроплан в момент фотографирования?
106. Миллион изделий
Изделие весит 89,4 г.
Сообразите в уме, сколько тонн весит миллион таких изделий.
107. Число путей
На рис. 127вы видите лесную дачу, разделенную просеками на квадратные кварталы. Штриховой линией обозначен путь по просекам от точки А до точки В. Это, конечно, не единственный путь между указанными точками по просекам.
Сколько можете вы насчитать различных путей одинаковой длины?

Рис. 127
108. Циферблат
Этот циферблат (рис. 128)надо разрезать на 6 частей любой формы, так, однако, чтобы сумма чисел, имеющихся на каждом участке, была одна и та же.
Задача имеет целью испытать не столько вашу находчивость, сколько быстроту соображения.
109. Восьмиконечная звезда
Числа от 1 до 16 надо расставить в точках пересечения линий фигуры, изображенной на рис. 129,так, чтобы сумма чисел на стороне каждого квадрата была 34 и сумма их на вершинах каждого квадрата также составляла 34.
110. Числовое колесо
Цифры от 1 до 9 надо разместить в фигуре на рис. 130так, чтобы одна цифра была в центре круга, прочие - у концов каждого диаметра и чтобы сумма трех цифр каждого ряда составляла 15.

Рис. 128
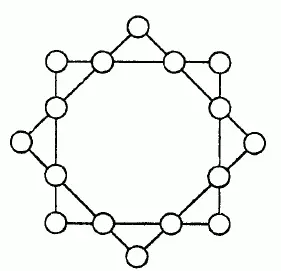
Рис. 129
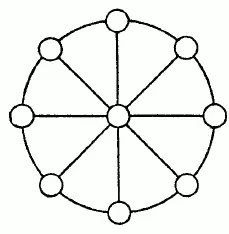
Рис. 130
111. Трехногий стол
Существует мнение, что стол о трех ногах никогда не качается, даже если ножки его и неравной длины. Верно ли это?
112. Какие углы?
Какие углы составляют между собой стрелки часов на рис. 131?
Ответ надо дать по соображению, не пользуясь транспортиром.
113. по экватору
Если бы мы могли обойти земной шар по экватору, то макушка нашей головы описала бы более длинный путь, чем каждая точка наших ступней.
Как велика эта разница?

Рис. 131. Какой величины углы между стрелками?
114. В шесть рядов
Вам известен, вероятно, шуточный рассказ о том, как девять лошадей расставлены были по десяти стойлам и в каждом стойле оказалась одна лошадь.
Задача, которая сейчас будет предложена, по внешности сходна с этой знаменитой шуткой, но имеет не воображаемое, а вполне реальное решение.
Читать дальше
Конец ознакомительного отрывка
Купить книгу




















