Яков Перельман - Живая математика. Математические рассказы и головоломки

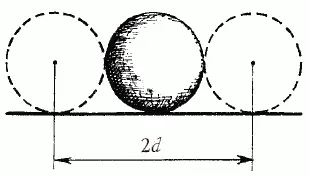
Рис. 26

Посмотрим теперь, как велика ширина мишени для центра движущегося шара при крокировке. Очевидно, что, если центр крокирующего приблизится к центру крокируемого меньше чем на радиус шара, удар обеспечен. Значит, ширина мишени в этом случае, как видно из рис. 26, равна двум диаметрам шара.

Итак, вопреки мнению игроков, при данных условиях вдвое легче попасть в шар, нежели свободно пройти ворота с самой лучшей позиции.

26. После сейчас сказанного эта задача не требует долгих разъяснений. Легко видеть (рис. 27), что ширина цели при крокировке равна двум диаметрам шара, т. е. 20 см; ширина же мишени при нацеливании в столбик равна сумме диаметра шара и столбика, т. е. 16 см (рис. 28). Значит, крокировать легче, чем заколоться в

20: 16 = 1 1/ 4раза,

всего на 25 %.

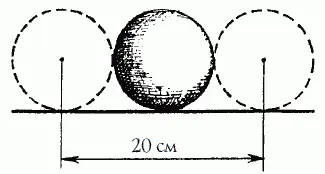
Рис. 27

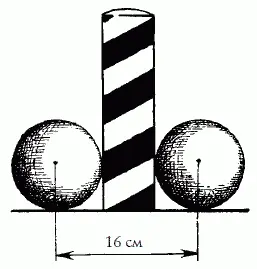
Рис. 28

Игроки же обычно сильно преувеличивают шансы крокировки по сравнению с попаданием в столбик.

27. Иной игрок рассудит так: раз ворота вдвое шире, чем шар, а столбик вдвое уже шара, то для свободного прохода ворот мишень вчетверо шире, чем для попадания в столбик.

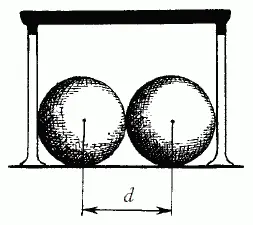
Рис. 29

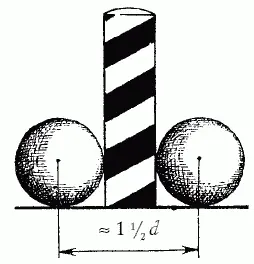
Рис. 30

Наученный предыдущими задачами, читатель наш подобной ошибки не сделает. Он сообразит, что для прицела в столбик мишень в 1 1/ 2раза шире, чем для прохода ворот с наилучшей позиции. Это ясно из рассмотрения рис. 29 и 30.

(Если бы ворота были не прямоугольные, а выгнутые дугой, проход для шара был бы еще уже - как легко сообразить из рассмотрения рис. 31.)

28. Из рис. 32 и 33 видно, что промежуток а , остающийся для прохода центра шара, довольно тесен при указанных в задаче условиях.

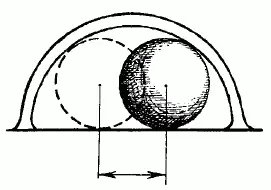
Рис. 31

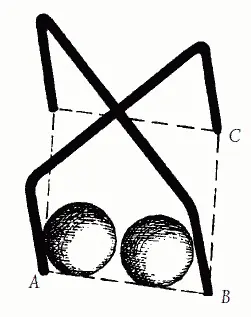
Рис. 32

Знакомые с геометрией знают, что сторона (АВ) квадрата меньше его диагонали (АС) приблизительно в 1,4 раза. Если ширина ворот 3 d (где d - диаметр шара), то АВ равно:

3d: 1,4 = 2, Id

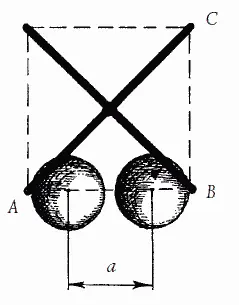
Рис. 33

Промежуток же а , который является мишенью для центра шара, проходящего мышеловку с наилучшей позиции, еще уже. Он на целый диаметр меньше и равен:

2,1 d - d = 1,1 d .

Между тем мишень для центра крокирующего шара равна, как мы знаем, 2d. Следовательно, крокировать почти вдвое легче при данных условиях, чем пройти мышеловку.

29. Мышеловка становится совершенно непроходимой в том случае, когда ширина ворот превышает диаметр шара менее чем в 1,4 раза. Это вытекает из объяснения, данного в предыдущей задаче. Если ворота дугообразные, условия прохождения еще сильнее ухудшаются.

- Еще веревочку? - спросила мать, вытаскивая руки из лоханки с бельем. - Можно подумать, что я вся веревочная. Только и слышишь: веревочку да веревочку. Ведь я вчера дала тебе порядочный клубок. На что тебе такая уйма? Куда ты ее девал?

- Куда девал бечевочку? - отвечал мальчуган. - Во-первых, половину ты сама взяла обратно…

- А чем же прикажешь мне обвязывать пакеты с бельем?

- Половину того, что осталось, взял у меня Том, чтобы удить в канаве колюшек.

- Старшему брату ты всегда должен уступать.

- Я и уступил. Осталось совсем немного, да из того еще папа взял половину для починки подтяжек, которые лопнули у него от смеха, когда случилась беда с автомобилем. А после - понадобилось еще сестре взять три пятых оставшегося, чтобы завязать свои волосы узлом…