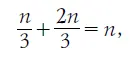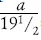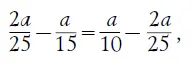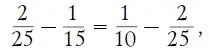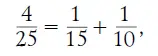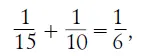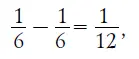Яков Перельман - Живая математика. Математические рассказы и головоломки

Сколько стоили покупки?

30. После того как мать взяла половину, осталась 1/ 2; после заимствования старшего брата осталась 1/ 4; после отца - 1/ 8; после сестры - 1/ 8х 3/ 5= 3/ 40. Если 30 см составляют 3/ 40первоначальной длины, то вся длина равна 30: 3/ 40= 400 см, или 4 м.

31. Так как число жителей городка неизвестно, то ответ на вопрос этой полушуточной головоломки возможен лишь в такой форме, достаточно, впрочем, определенной: «Требуется столько штук сапог, сколько в городке жителей».

В самом деле. Пусть число жителей равно п. Тогда для снабжения одноногих требуется n/ 3штук сапог. Из прочих 2n/з жителей нуждается в обуви только половина - 1/ 3; а так как каждому из этой части населения нужно по два сапога, то им требуется 2/ 3штук. Всего же для городка следует заготовить

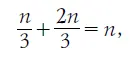
т. е. столько штук, сколько в городке жителей.

32. Позже всего выпадает, конечно, тот волос, который сегодня моложе всех, т. е. возраст которого 1 день. Посмотрим же, через сколько времени дойдет до него очередь выпасть. В первый месяц из тех 150 000 волос, которые сегодня имеются на голове, выпадет 3 тысячи, в первые два месяца - 6 тысяч, в течение первого года - 12 раз по 3 тысячи, т. е. 36 тысяч. Пройдет, следовательно, четыре года с небольшим, прежде чем наступит черед выпасть последнему волосу. Так определилась у нас средняя долговечность человеческого волоса: четыре с небольшим года.

33. Многие, не подумав, отвечают: 200 руб. Это неверно: ведь тогда основная зарплата будет больше сверхурочных только на 150 руб., а не на 200.

Задачу нужно решать так. Мы знаем, что если к сверхурочным прибавить 200 руб., то получим основную зарплату. Поэтому если к 250 руб. прибавим 200 руб., то у нас должны составиться две основные зарплаты. Но 250 + 200 = 450. Значит, двойная основная зарплата составляет 450. Отсюда одна зарплата без сверхурочных равна 225 руб., сверхурочные же составят остальное от 250 руб., т. е. 25 руб.

Проверим: зарплата, 225 руб., больше сверхурочных, т. е. 25 руб., на 200 руб., - как и требует условие задачи.

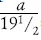
34. Эта задача любопытна в двух отношениях: во-первых, она легко может внушить мысль, что искомая скорость есть средняя между 10 км и 15 км в час, т. е. равна 12 1/ 2км в час. Нетрудно убедиться, что такая догадка неправильна. Действительно, если длина пробега а километров, то при 15-километровой скорости лыжник будет в пути а/ 15 часов, при 10-километровой - a/ 10, при 12 1/ 2-километровой -, или 2a/ 25. Но тогда должно существовать равенство

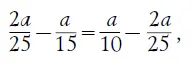
потому что каждая из этих разностей равна одному часу. Сократив на а, имеем

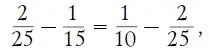
или, по свойству арифметической пропорции:

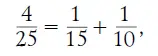
равенство неверное:

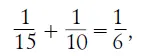
т. е. 4/ 24, а не 4/ 25.

Вторая особенность задачи та, что она может быть решена не только без помощи уравнений, но даже просто устным расчетом.

Рассуждаем так. Если бы при 15-километровой скорости лыжник находился в пути на два часа дольше (т. е. столько же, сколько при 10-километровой), то он прошел бы путь на 30 км больший, чем прошел в действительности. В один час, мы знаем, он проходит на 5 км больше; значит, он находился бы в пути 30: 5 = 6 ч. Отсюда определяется продолжительность пробега при 15-километровой скорости: 6-2 = 4 ч. Вместе с тем становится известным и проходимое расстояние:

15 х 4 = 60 км.

Теперь легко уже найти, с какой скоростью должен лыжник идти, чтобы прибыть на место ровно в полдень, - иначе говоря, чтобы употребить на пробег 5 час.

60: 5 = 12 км.

Легко убедиться испытанием, что этот ответ правилен.

35. Задачу можно решить, не обращаясь к уравнению, и притом различными способами.

Вот первый прием. Молодой рабочий проходит за 5 мин 1/ 4пути, старый - 1/ 6пути, т. е. меньше, чем молодой, на

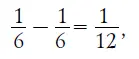
Так как старый опередил молодого на 1/ 6пути, то молодой настигнет его через