Яков Перельман - Живая математика. Математические рассказы и головоломки

Рис. 15

Нормальное расположение шашек (положение I)

Рис. 16.

Неразрешимый случай (положение II)

В пределах этого шестиместного участка всегда можно привести на нормальные места шашки 10, 11, 12. Когда это достигнуто, то в последнем ряду шашки 14 и 15 окажутся размещенными либо в нормальном порядке, либо в обратном (рис. 16).Таким путем, который читатели легко могут проверить на деле, мы приходим к следующему результату.

Любое начальное положение может быть приведено к расположению либо рис. 15(положение I), либо рис. 16(положение II).

Если некоторое расположение, которое для краткости обозначим буквою S, может быть преобразовано в положение I, то, очевидно, возможно и обратное - перевести положение I в положение S. Ведь все ходы шашек обратимы: если, например, в схеме I мы можем шашку 12 поместить на свободное поле, то можно ход этот тотчас взять обратно противоположными движениями.

Итак, мы имеем две серии расположений таких, что положения одной серии могут быть переведены в нормальное I, а другой серии - в положение II. И, наоборот, из нормального расположения можно получить любое положение первой серии, а из расположения II - любое положение второй серии. Наконец, два любых расположения, принадлежащие к одной и той же серии, могут быть переводимы друг в друга.

Нельзя ли идти дальше и объединить эти два расположения - I и II? Можно строго доказать (не станем входить в подробности), что положения эти не превращаются одно в другое никаким числом ходов. Поэтому все огромное число размещений шашек распадается на две разобщенные серии: 1) на те, которые могут быть переведены в нормальное I: это - положения разрешимые; 2) на те, которые могут быть переведены в положение II и, следовательно, ни при каких обстоятельствах не переводятся в нормальное расположение: это - положения, за разрешение которых назначались огромные премии.

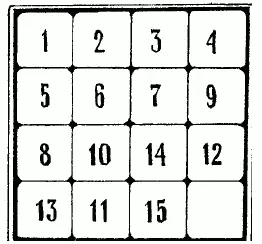
Рис. 17. Шашки не приведены в порядок

Как узнать, принадлежит ли заданное расположение к первой или ко второй серии? Пример разъяснит это.

Рассмотрим расположение, представленное на рис. 17.Первый ряд шашек в порядке, как и второй, за исключением последней шашки (9). Эта шашка занимает место, которое в нормальном расположении принадлежит 8. Шашка 9 стоит, значит, ранее шашки 8: такое упреждение нормального порядка называют «беспорядком». О шашке 9 мы скажем: «Здесь имеет место 1 беспорядок». Рассматривая дальнейшие шашки, обнаруживаем упреждение для шашки 14; она поставлена на три места (шашек 12, 13, 11) ранее своего нормального положения; здесь у нас 3 беспорядка (14 ранее 12; 14 ранее 13; 14 ранее 11). Всего мы насчитали уже 1 + 3=4 беспорядка. Далее, шашка 12 помещена ранее шашки 11, и точно так же шашка 13 - ранее шашки 11. Это дает еще 2 беспорядка. Итого, имеем 6 беспорядков. Подобным образом для каждого расположения устанавливают общее число беспорядков, освободив предварительно последнее место в правом нижнем углу. Если общее число беспорядков, как в рассмотренном случае, четное, то заданное расположение может быть приведено к нормальному конечному; другими словами, оно принадлежит к разрешимым. Если же число беспорядков нечетное, то расположение принадлежит ко второй серии, т. е. к неразрешимым (ноль беспорядков принимается за четное число их).

Благодаря ясности, внесенной в эту игру математикой, прежняя лихорадочная страсть в увлечении сейчас совершенно немыслима. Математика создала исчерпывающую теорию игры, теорию, не оставляющую ни одного сомнительного пункта. Исход игры зависит не от каких-либо случайностей, не от находчивости, как в других играх, а от чисто математических факторов, предопределяющих его с безусловной достоверностью».

Обратимся теперь к головоломкам в этой области. Вот несколько разрешимых задач, придуманных изобретателем игры.

Исходя из расположения, показанного на рис. 15, привести шашки в правильный порядок, но со свободным полем в левом верхнем углу (рис. 18).

Рис. 18. К первой задаче Самуэля Лойда