Яков Перельман - Математика для любознательных

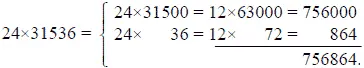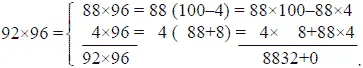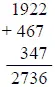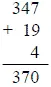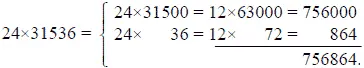
Остается лишь приписать три нуля - и мы имеем искомый результат: 756.864.000.

Мы упоминали раньше, что для выполнения тех отдельных действий умножения, на которые распадается каждый из указанных выше приемов, существуют также удобные способы. Некоторые из них весьма несложны и удобоприменимы; они настолько облегчают вычисления, что мы советуем читателю вообще запомнить их, чтобы пользоваться при обычных расчетах. Таков, например, прием перекрестного умножения, весьма удобный при действии с двузначными числами. Способ этот не нов; он восходит к грекам и индусам и в старину назывался «способом молнии», или «умножением крестиком». Теперь он хорошо забыт, и о нем не мешает напомнить [75].

Пусть дано перемножить 24 x 32. Мысленно располагаем числа по следующей схеме, одно под другим:

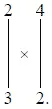
Теперь последовательно производим следующие действия:

1) 4 x 2 = 8- это последняя цифра результата.

2) 2 x 2 = 4; 4 x 3 = 12; 4 + 12 = 16; 6- предпоследняя цифра результата; 1 запоминаем.

3) 2 x 3 = 6, да еще удержанная в уме 1-ца, имеем 7 - это первая цифра результата.

Получаем все цифры произведения: 7, 6, 8 - 768. После непродолжительного упражнения прием этот усваивается очень легко.

Другой способ, состоящий в употреблении так называемых «дополнений», удобно применяется в тех случаях, когда перемножаемые числа близки к 100.

Предположим, что требуется перемножить 92 x 96. «Дополнение» для 92 до 100 будет 8; для 96-ти - 4. Действие производят по следующей схеме:

множители: 92 и 96

дополнения: 8 и 4.

Первые две цифры результата получаются простым вычитанием из множителя «дополнения» множимого или наоборот; т. е. из 92-х вычитают 4, или из 96-ти - 8. В том и другом случае имеем 88; к этому числу приписывают произведение «дополнений»: 8 x 4 = 32. Получаем результат 8832.

Что полученный результат должен быть верен, наглядно видно из следующих преобразований:

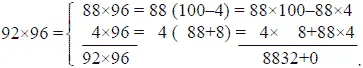
Умение быстро определять день недели, на какой приходится та или иная дата (например, 17 января 1893 г., 4 сентября 1943 г. и т. п.), основано на знании особенностей нашего календаря, которые мы сейчас и изложим.

1-е января 1-го года нашей эры приходилось (это установлено расчетом) на субботу. Так как в каждом простом году 365 дней, или 52 полных недели и 1 день, то год должен кончаться тем же днем недели, каким начался; поэтому последующий год начинается одним днем недели позже, чем предыдущий. Если 1 января 1-го года была суббота, то 1января 2-го года было днем позже, т. е. воскресенье, 3-го года - на 2 дня позже; а 1 января, например, 1923-го года было бы на 1922 дня (1923-1) после субботы, - если бы не было ни одного високосного года. Число високосных лет мы найдем, разделив 1923 на 4 = 480; но отсюда, для нового стиля [76], надо исключить календарную разницу в 13 дней: 480-13 = 467. К полученному числу надо прибавить число дней, протекших после 1 января 1923-го года до определяемой даты - скажем для примера, до 14 декабря: это составит 347 дней.

Сложив 1922, 467 и 347, мы делим сумму на 7 и по полученному остатку 6 определяем, что 14 декабря 1923-го года при ходилось на 6 день после субботы, - а именно на пятницу.

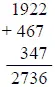
Такова сущность вычислений недельного дня любой даты. На практике дело значительно упрощается. Прежде всего заметим, что в течение каждого 28-летнего периода бывает, вообще говоря, 7 високосных лет (неделя), - так что каждые 28 лет день недели любой даты должен повторяться. Кроме того вспомним, что в предыдущем примере мы вычли из 1923 сначала 1, а затем календарную разницу обоих стилей, т. е. 13, всего 1 + 13 = 14 дней, или две полных недели. Но полное число недель, понятно, не влияет на результат. Поэтому для дат XX века надо принимать во внимание только: 1) число дней, протекших с 1 января данного года - в нашем примере 347; затем 2) прибавить число дней, соответствующее остатку лет от деления 1923 на 28, и, наконец, 3) число високосных лет в этом остатке, т. е. 4. Сумма этих трех чисел (347 + 19 + 4), т. е. 370, дает при делении на 7 тот же остаток 6 (пятница), который был получен нами раньше.

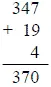
Таким же образом мы найдем, что 15 января 1923 г. приходилось на понедельник (14 + 19 + 4 = 37; 37: 7 - в остатке 2). Для 9 февраля нов. ст. 1917 г. мы нашли бы 39 + 13 + 3 = 55; при делении 55 на 7 получаем в остатке 6 - пятница. Для 29 февраля нов. ст. 1904 г.: 59 + 0-1 [77]= 58; остаток от деления на 7 здесь 2 - понедельник.