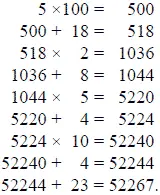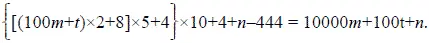Яков Перельман - Математика для любознательных

А именно: порядковый номер месяца (май, 5-й месяц) я прошу вас умножить на 100, прибавить к произведению число месяца (18), сумму удвоить, к результату прибавить 8, полученное число умножить на 5, к произведению прибавить 4, помножить результат на 10, прибавить 4 и к полученному числу прибавить ваш возраст (23).

Когда вы все это проделаете, вы сообщаете мне окончательный результат вычислений. Я вычитаю из него 444, а разность разбиваю на грани, справа налево, по 2 цифры в каждой: получаю сразу как день и месяц вашего рождения, так и ваш возраст.

Действительно. Проделаем последовательно все указанные вычисления:

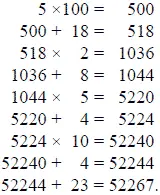
Произведя вычитание 52267-444, получаем число 51823.

Теперь разобьем это число на грани, справа налево, по две цифры в каждой. Имеем:

5-18-23,

т. е. 5-го месяца (мая), числа 18; возраст 23 года.

Почему же так получилось?

Секрет нашего фокуса легко понять из рассмотрения следующего равенства:

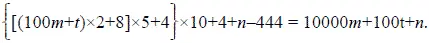
Здесь буква m обозначает порядковый номер месяца, t - число месяца, n - возраст. Левая часть равенства выражает все последовательно произведенные вами действия, а правая - то, что должно получиться, если раскрыть скобки и проделать возможные упрощения. В выражении 10000m + 100t + n ни m, ни t, ни n не могут быть более чем двузначными числами; поэтому число, получающееся в результате, всегда должно при делении на грани, по две цифры в каждой, распасться на три части, выраженные искомыми числами m, t и n.

Предоставляем изобретательности читателя придумать видоизменения этого фокуса, т. е. другие комбинации действий, дающие подобный же результат.

Читателю же предлагаю раскрыть также секрет следующего незамысловатого фокуса, который описан еще в «Арифметике» Магницкого, в главе: «Об утешных некиих действиях через арифметику употребляемых».

Пусть кто-либо задумает какое-нибудь число, относящееся к деньгам, к дням, к часам или к «каковой-либо иной числимой вещи». Остановимся на примере перстня, надетого на 2-й сустав мизинца (т. е. 5-го пальца) 4-го из 8 человек. Когда в это общество является отгадчик, его спрашивают: у кого из восьми человек (обозначенных номерами от 1 до 8) на каком пальце и на котором суставе находится перстень?

«Он же рече: кто-либо от вас умножи оного, который взял через 2, и к тому приложи 5, потом паки (снова) умножи чрез 5, также приложи перст на нем же есть перстень (т. е. к полученному прибавь номер пальца с перстнем). А потом умножи чрез 10, и приложи сустав на нем же перстень взложен, и от сих произведенное число скажи ми, по немуже искомое получиши.

Они же твориша (поступили) якоже повеле им, умножаху четвертого человека, который взял перстень, и прочая вся, яже велеше им; якоже явлено есть (см. выкладки на стр. 255); из всего собрания пришло ему число 702, из него же он вычитал 250, осталось 452, т. е. 4-й человек, 5-й палец, 2-й сустав».

Не надо удивляться, что этот арифметический фокус был известен еще 200 лет назад: задачи совершенно подобного же рода я нашел в одном из первых сборников математических развлечений, именно у Баше-де-Мезирьяка, в его книге «Занимательные и приятные числовые задачи», вышедшей в 1612 г.; а туда она попала из сочинения Леонарда Пизано (1202 г.). Нужно вообще заметить, что большая часть математических игр, головоломок и развлечений, которые в ходу в настоящее время, очень древнего происхождения.

Кому приходилось присутствовать на сеансах нашего русского вычислителя Арраго, тот, без сомнения, не мог не поразиться его изумительными счетными способностями. Тут уж перед нами не фокус, а редкое природное дарование. Не существует «трюков» для выполнения в уме таких выкладок, как возвышение в куб любого четырехзначного числа или умножение любого шестизначного числа на шестизначное. Куб числа 4729, например, Арраго вычислил при мне в уме менее чем в одну минуту (результат 105756712489), а на умножение 679321x887064, также в уме, употребил всего 1 1/ 2минуты (результат 602601203544).