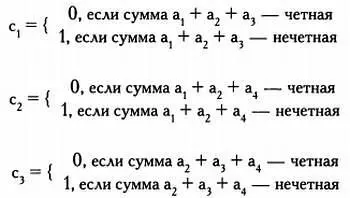Жуан Гомес - Мир математики. т.2. Математики, шпионы и хакеры. Кодирование и криптография

11011 2= 1∙2 4+ 1∙2 3+ 0∙2 2+ 1∙2 1+ 1∙2 0.

Если мы вычислим выражение, стоящее справа от знака равенства, мы получим 27, что является десятичной формой двоичного числа 11011. Для обратного перехода мы последовательно делим десятичное число на 2 (основание двоичной системы) и записываем остатки, пока не получим частное 0. Двоичное число будет иметь в качестве первой цифры последнее ненулевое частное, а следующими цифрами будут полученные остатки, начиная с последнего. Например, переведем десятичное число 76 в двоичный вид.

Разделим 76 на 2, получим частное 38 и остаток 0.

Разделим 38 на 2, получим частное 19 и остаток 0.

Разделим 19 на 2, получим частное 9 и остаток 1.

Разделим 9 на 2, получим частное 4 и остаток 1.

Разделим 4 на 2, получим частное 2 и остаток 0.

Разделим 2 на 2, получим частное 1 и остаток 0.

Разделим 1 на 2, получим частное 0 и остаток 1.

Остаток от деления записываем в обратном порядке. Таким образом, число 76 выглядит в двоичной системе как 1001100 2. Этот результат можно проверить по таблице ASCII (в таблице слева приписан дополнительный 0, чтобы получить строки из четырех цифр). Выражение числа, записанного в одной системе счисления, в другой системе называется переходом к другому основанию.

Описанные выше коды обеспечивают безопасную и эффективную связь между компьютерами, программами и пользователями. Но этот онлайновый язык основан на общей теории информации, которая лежит в основе процесса коммуникации.

Первый шаг в этой теории является настолько очевидным, что его легко упустить из вида: как измерить информацию.

Такая простая фраза, как «Приложение размером 2 КБ», основана на блестящих идеях, которые впервые появились в статье «Математическая теория связи», опубликованной в двух частях в 1948 г. американским инженером Клодом Шенноном.

В этой основополагающей статье Шеннон предложил использовать слово «бит» для обозначения наименьшей единицы информации. Общая проблема, которую Шеннон рассматривал в своей работе, знакома и современным читателям. Как лучше всего зашифровать сообщение, чтобы оно не повредилось во время передачи? Шеннон пришел к выводу, что невозможно найти шифр, который предотвратит потерю информации. Иными словами, при передаче информации неизбежно возникают ошибки. Однако этот вывод не помешал поиску стандартов кодификации, которые, не имея возможности исключить ошибки, могли бы по крайней мере обеспечить высокий уровень надежности.

При цифровой передаче информации сообщение, сгенерированное отправителем (это может быть как человек, так и компьютер или другое устройство), кодируется в двоичной системе и поступает в канал связи, состоящий из компьютеров отправителя и получателя, плюс самой линии связи, которая может быть или физическим кабелем, или беспроводной (радиоволны, инфракрасное излучение и т. д.). Движение по каналу связи является особенно уязвимым процессом, потому что сообщение подвергается всевозможным воздействиям, в том числе взаимодействиям с другими сигналами, неблагоприятным температурам физической среды и затуханиям (ослаблению) сигнала при прохождении через среду. Эти источники помех называются шумами.

Одним из таких методов является избыточность информации. Он состоит в повторении при определенных критериях некоторых характеристик сообщения. Рассмотрим пример, который поможет пояснить процесс. Возьмем текст, в котором каждое слово состоит из четырех битов, общее количество различных слов — 16 (т. к. 2 4= 16), каждое слово имеет вид а 1а 2а 3а 4. Перед отправкой сообщения мы добавим к слову еще три бита c 1c 2c 3 так что закодированное сообщение при движении по каналу связи будет выглядеть как а 1а 2а 3а 4c 1c 2c 3. Дополнительные символы c 1c 2c 3обеспечивают надежность сообщения. Они называются контрольными битами, или битами четности, и строятся следующим образом.

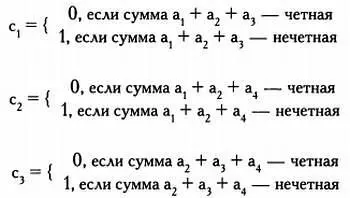
Добавим следующие биты четности к сообщению 0111.

Так как сумма 0 + 1 + 1 = 2 четная, с 1= 0.

Так как сумма 0 + 1 + 1 = 2 четная, с 2= 0.

Так как сумма 1 + 1 + 1 = 3 нечетная, с 3= 1.

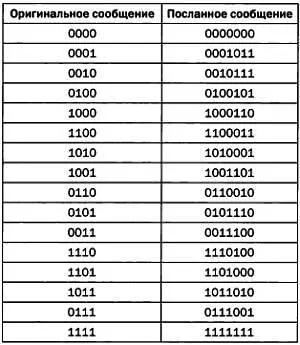
Следовательно, сообщение 0111 будет передано в виде 0111001. Для «слов» мы, таким образом, получим следующую таблицу:

* * *