Игра в шпионов
При каких условиях сообщение, зашифрованное аффинным шифром, может расшифровать предполагаемый получатель или шпион? Мы ответим на этот вопрос, используя простой пример шифра для алфавита из шести букв:

Текст будет зашифрован с помощью аффинного шифра C(x)= 2x+ 1 (mod 6).
Буква Азашифрована по формуле С(0) = 2 х 0 + 1 1 (mod 6), что соответствует букве В.
Буква Взашифрована по формуле C(1) = 2 x 1 + 1 3 (mod 6), что соответствует букве D.
Буква Сзашифрована по формуле С(2) = 2 х 2 + 1 5 (mod 6), что соответствует букве F.
Буква Dзашифрована по формуле С(3) = 2 х З + 1 = 7 1 (mod 6), что соответствует букве В.
Буква Езашифрована по формуле С(4) = 2 х 4 + 1 = 9 3 (mod 6), что соответствует букве D.
Буква Fзашифрована по формуле С(5) = 2 х 5 + 1 = 11 5 (mod 6), что соответствует букве F.
Предлагаемый аффинный шифр преобразует сообщения АВС и DEF в одно и то же BDF, поэтому исходное сообщение теряется. Что же случилось?
Если мы работаем с шифром, выраженным формулой С (а, b)(х)= (а∙ х+ b) (mod n), мы можем расшифровать сообщение однозначно, только когда НОД ( а, n) = 1. В нашем примере НОД (2, 6) = 2 и, следовательно, не удовлетворяет этому условию.
Математическая операция расшифровки эквивалентна нахождению неизвестного хпри данном значении упо модулю n.
С (а, b)(х) = (ах+ b)= y (mod n)
(ах+ b)= у (mod n)
ах— у— b (mod n)
Другими словами, нам нужно найти значение а -1(обратное значению а ), удовлетворяющее равенству а -1а= 1, так что
а -1 ах= а -1 х(у— b)(mod n)
х= а -1 (у— b)(mod n).
Следовательно, для успешной расшифровки мы должны найти число, обратное числу а по модулю n , и, чтобы не тратить зря время, мы должны заранее знать, существует ли это обратное число.
В случае аффинного шифра С (а, b)(х)= (ах+ b) (mod n)обратное значение числа абудет существовать тогда и только тогда, когда НОД ( а, n) = 1.
В случае аффинного шифра в нашем примере, С(х)= 2х+ 1 (mod 6), мы хотим узнать, существует ли обратное значение для числа а, в нашем случае для числа 2.
То есть существует ли целое число n, которое меньше 6 и удовлетворяет выражению 2∙ n= 1 (mod 6). Для ответа на этот вопрос мы подставим в данное выражение все возможные значения (0, 1, 2, 3, 4, 5):
2-0 = 0, 2–1 = 2, 2–2 = 4, 2–3 = 6 0, 2–4 = 8 2, 2–5 = 10 4.
Нет такого значения, следовательно, можно заключить, что 2 не имеет обратного числа. На самом деле мы это уже знали, так как НОД (2,6) 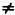 1.
1.
Предположим теперь, что мы перехватили зашифрованное сообщение: YSFMG. Мы знаем, что оно было зашифровано аффинным шифром вида С( х) = 2 х+ 3 и изначально было написано на испанском языке с алфавитом из 27 букв (включая букву N, идущую после обычной N).
Как получить исходное сообщение?
Сначала мы посчитаем НОД (2,27), который равен 1. Значит, сообщение можно расшифровать! Для этого для функции С( х) = 2 х+ 3 мы должны найти обратную функцию по модулю 27:
у= 2х+ 3
2х= у— 3.
Чтобы найти x, мы должны умножить обе части уравнения на число, обратное 2.
Число, обратное числу 2 по модулю 27, — это целое число n такое, что 2 n 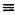 1 (mod 27), а именно 14. И действительно:
1 (mod 27), а именно 14. И действительно:
14∙2 = 28 1.
Итак, мы имеем
x = 14∙(у— 3).
Теперь мы можем расшифровать сообщение YSFMG.
Буква Yстоит на позиции 25, ей соответствует расшифрованная буква, стоящая на позиции
14∙(25—3) = 308 11 (mod 27).
Буква, стоящая в алфавите на позиции 11, — это L.
Для буквы Sимеем 14∙(19—3) = 224 8 (mod 27), эта позиция соответствует букве I.
Для буквы Fимеем 14∙(5–3) = 28 1 (mod 27), что соответствует букве В.
Для буквы Мимеем 14∙(12—3) = 126 18 (mod 27), что соответствует букве R.
Для буквы Gимеем 14∙(6–3) = 42 15 (mod 27), что соответствует букве О.
Читать дальше


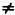 1.
1.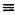 1 (mod 27), а именно 14. И действительно:
1 (mod 27), а именно 14. И действительно:










