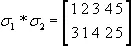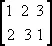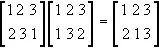Хавьер Фресан - Мир математики - m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

Тогда в композиции σ 1* σ 2числу 1 ставится в соответствие 3. Теперь посмотрим, что произойдет с числом 2: при перестановке σ 2ему на смену придет 4, при перестановке σ 14 соответствует 1, следовательно, в композиции перестановок σ 1* σ 2числу 2 ставится в соответствие число 1. Продолжив рассуждения, получим

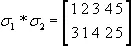
Эта композиция перестановок полностью удовлетворяет всем условиям, приведенным в определении группы. Таким образом, мы получили симметрическую группу Sn, где n — число элементов множества, к которому применяется перестановка.

ЛЕВИ-СТРОСС: А где используются эти группы?

ВЕЙЛЬ: Повсеместно! Между прочим, существует теорема, согласно которой любая конечная группа содержится в некоторой симметрической группе — достаточно верно выбрать число элементов группы. Более того, мы, сами того не осознавая,

55

уже работали с симметрической группой. Помните, как мы различали преобразования треугольника? Мы пронумеровали его вершины и рассмотрели, как они меняются местами при различных движениях. Получается, что преобразование треугольника — не более чем перестановка чисел 1, 2 и 3. К примеру, после поворота R первая вершина будет находиться там, где раньше располагалась вторая, следовательно, при этой перестановке 1 ставится в соответствие 2. Аналогично, вершины 2 и 3 будут находиться там, где раньше располагались 3 и 1 соответственно, таким образом, при этой перестановке 3 соответствует 2, 1—3. Следовательно, поворот R описывается той же информацией, что и

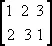
Повторим рассуждения для каждого преобразования и получим следующую таблицу соответствий.

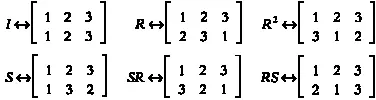
Обратите внимание, что если мы составим композицию перестановок

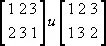
которые, как мы только что показали, обозначают R и S соответственно, то получим следующую перестановку:

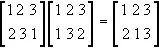
которая соответствует RS. Перестановки и преобразования треугольника в точности соответствуют друг другу! С точки зрения структуры группа преобразований, оставляющих треугольник неизменным, идентична симметрической группе S 3Говорят, что эти две группы изоморфны.

56

В общем случае группы G и Н называются изоморфными, если существует функция f, которая сопоставляет каждому элементу G некий элемент Н так, что выполняются три следующих условия:

1) различным элементам соответствуют различные отображения;

2) любой элемент Н является отображением некоторого элемента G;

3) функция f удовлетворяет определению групповой операции, а именно: если мы выполним операцию над элементами g 1и g 2множества G, после чего найдем отображение ее результата или же если мы сначала найдем отображения f(g 1) и f(g 2), после чего выполним операцию над ними, то полученные результаты будут одинаковы [5] 1 Понятие изоморфизма групп подробно рассматривается в начале приложения. .

ЛЕВИ-СТРОСС: Прекрасно, что дальше?

ВЕЙЛЬ: Аксиомы, определяющие структуру группы, можно использовать при доказательстве теорем, которые будут верны для любых групп при соблюдении необходимых условий. В частности, эти теоремы будут верны для нашей группы преобразований треугольника! Пункт 2 определения группы гласит, что существует нейтральный элемент е такой, что равенство а*е = е*а = а верно для любого а, и в определении не указывается, сколько элементов группы обладают этим свойством. Но в пункте 3 определения подразумевается, что он единственный — в противном случае потребовалось бы уточнить, какому из нейтральных элементов равна композиция произвольного элемента и обратного ему. Докажем, что нейтральный элемент является единственным. Допустим, что существуют два нейтральных элемента, е 1и е 2. Требуется доказать, что е 1= е 2. Рассмотрим произведение е 1* е 2.

С одной стороны, е 1— нейтральный элемент, поэтому он не изменяет значение элемента, записанного слева от него. Следовательно, е 1* е 2= е 2. С другой стороны, е 2— также нейтральный элемент, следовательно, при умножении любого элемента на е 2этот элемент не изменится. Таким образом, е 1* е 2= е 1Мы доказали, что е 1* е 2одновременно равняется е 1и е 2, следовательно, е 1и е 2должны быть равны.