Хавьер Фресан - Мир математики - m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

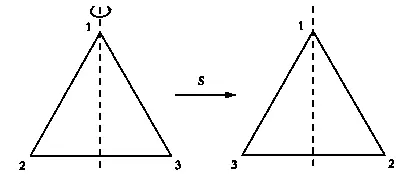
Результат симметрии S.

Теперь нам известны преобразования R и S. Что с ними можно сделать?

ЛЕВИ-СТРОСС: Выполнить сначала первое, а затем — второе?

ВЕЙЛЬ: Именно! Основное свойство этих преобразований заключается в том, что для двух таких преобразований можно определить их композицию. Применим поворот R, затем — симметрию S и обозначим полученный результат как SR. Мы привыкли читать слева направо, поэтому было бы логичнее записать RS, так как поворот R выполняется первым. Однако обозначение SR имеет свои преимущества.

Найдем композицию двух исходных преобразований.

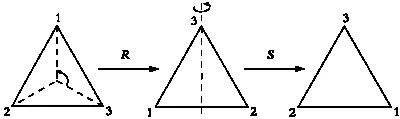
Композиция преобразований R и S.

На рисунке показано, что при движении SR вторая вершина остается неизменной, а две другие меняются местами. Следовательно, порядок следования вершин меняется с 1—2—3 на 3—2—1. Обратите внимание, что этот же результат можно

45

получить, применив к исходному треугольнику осевую симметрию, ось которой проходит через вторую вершину. Два этих преобразования совпадают.

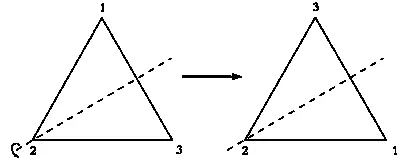
Композиция преобразований SR представляет собой симметрию.

Теперь определим RS, то есть сначала применим S, а затем R, и посмотрим, как изменится порядок вершин.

ЛЕВИ-СТРОСС: Но от перемены мест множителей произведение не меняется.

ВЕЙЛЬ: Ах, эта юность, эта святая простота! Как же сложно по-новому посмотреть на то, что всем известно с детства. «От перемены мест множителей произведение не меняется» только при умножении чисел: трижды семь — то же, что и семью три. Однако нет никакой причины, по которой этот закон должен выполняться для других операций, например для сочетания движений, оставляющих исходную фигуру неизменной. Между прочим, это четко видно в нашем примере. Если сначала мы выполним S, а затем R, то получим...

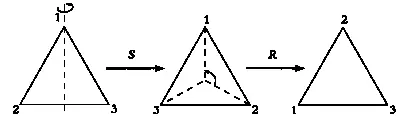
Композиция преобразований S и R.

Вершины будут располагаться в порядке 2—1—3. Таким образом, результаты движений SR и RS отличаются.

46

ЛЕВИ-СТРОСС: Но RS — тоже симметрия.

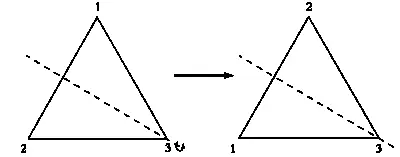
Преобразование RS — симметрия.

ВЕЙЛЬ: Да, и ее ось проходит через третью вершину. Для того чтобы при симметрии треугольник оставался неизменным, ось симметрии должна проходить через его центр и одну из вершин. На основе R и S можно определить все возможные разновидности такой симметрии. Если ось симметрии проходит через вторую вершину, это симметрия SR, если через третью — RS. Добавив к ним собственно симметрию S, ось которой проходит через первую вершину, получим полный перечень:

S, SR и RS — все возможные виды симметрии, оставляющие треугольник неизменным.

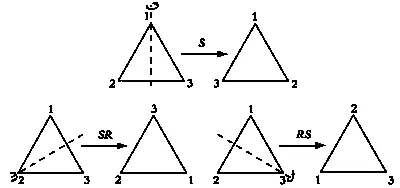
Виды симметрии, оставляющие треугольник неизменным.

ЛЕВИ-СТРОСС: Послушайте, господин Вейль, чтобы мы могли составить композицию двух преобразований, они обязательно должны отличаться?

47

ВЕЙЛЬ: Вовсе нет. Ничто не мешает применить одно и то же преобразование несколько раз подряд. Так как поворот фигуры два раза подряд на 120° равносилен повороту на 240°, движение RR также будет поворотом, при котором треугольник остается неизменным. Вместо RR будем записывать R 2. Если мы повернем фигуру еще на 120°, она совпадет с исходной. Таким образом, R3 никак не изменяет треугольник. Мы не учли преобразование, которое оставляет порядок следования вершин неизменным — 1—2—3. Будем называть это преобразование тождественным и обозначим его через I. Обратите внимание, что композицией тождественного преобразования и любого другого движения будет это движение.

Мы доказали, что R 3= I, так как результатом трех поворотов является исходная фигура. Говорят, что порядок R равен трем. В общем случае порядок преобразования указывает, сколько раз его нужно применить, чтобы получить тождественное преобразование. S имеет порядок, равный двум — если мы повторим симметрию дважды, то получим исходный треугольник. Мы уже показали, что S, RS и SR — симметрии треугольника. Какие повороты оставляют фигуру неизменной? Обратите внимание, что поворот обладает этим свойством только тогда, когда угол поворота кратен 120°. Следовательно, все возможные повороты — это R, R 2и R 3= I.