Хавьер Фресан - Мир математики - m. 35 Пока алгебра не разлучит нас. Теория групп и ее применение.

Якобсон прослушал несколько моих курсов, я — несколько курсов, которые вел он. По окончании занятий мы обычно продолжали разговор в одном из ближайших кафе. Якобсон, подобно древним грекам, любил застольные беседы. Он всегда, даже в научной работе, предпочитал диалог монологу, поэтому выполнил множество совместных исследований с разными учеными. К примеру, мы с ним вместе подготовили комментарий к «Кошкам» Бодлера, где «любовник пламенный» противопоставляется

40

тому, «кому был ведом лишь зов познания», и двух героев стихотворения объединяет исключительно любовь к кошкам. Мне кажется, это был единственный случай, когда в журнале по антропологии был опубликован анализ французского стихотворения XIX века. Но Якобсон не просто любил диалог — он обладал особым даром вдохновлять собеседников, с которыми неизменно был на ты. Не важно, о чем шла речь — о русском формализме или о взаимосвязи генетического и лингвистического кодов, — с ним любой ощущал себя, как сказал Исайя Берлин, словно на восходящей кривой: более чувствительным и интересным, чем на самом деле.

Интересно, где сейчас Якобсон. Ему следовало бы присоединиться к нам!

ВЕЙЛЬ: Возможно, мы бы поспорили о том, кто знает больше языков.

ЛЕВИ-СТРОСС: В этом споре вам бы пришлось нелегко — он в совершенстве владел шестью или семью языками. Мне кажется, вы славно бы повеселились.

Между прочим, именно Якобсон вдохновил меня написать «Элементарные структуры родства» по окончании курса по этой теме, который я прочел зимой 1942-го.

Именно тогда я решил проследовать в этнологии тем же путем, что Якобсон с коллегами — в лингвистике. Но мне кажется, мы не сможем продолжить нашу беседу, если вы не расскажете мне, о чем же говорится в этой теории групп, которая вам так хорошо знакома.

41

ВЕЙЛЬ: Присаживайтесь, господин Леви-Стросс.

ЛЕВИ-СТРОСС: Вы объясните мне, что такое группа?

ВЕЙЛЬ: Постараюсь. Мне хотелось бы начать с одного примера — он очень прост, но в нем постепенно раскрывается большинство основных понятий теории групп. Представьте себе равносторонний треугольник — надеюсь, вы помните, что это треугольник, все стороны которого равны. Меня интересуют движения, которые не меняют положение треугольника, то есть такие, когда сторонний наблюдатель не сможет увидеть разницу между треугольниками «до» и «после». Говорят, что треугольник инвариантен относительно таких преобразований.

ЛЕВИ-СТРОСС: Простите, я перебью вас, господин Вейль. Я кое-что не понял: если фигура в результате этих преобразований не меняется, то как определить, выполнили мы это преобразование или нет? Ведь треугольники не имеют памяти!

ВЕЙЛЬ: Хороший вопрос. Я как раз собирался ответить на него. Нужно пронумеровать вершины треугольника. Он будет выглядеть так же, однако в результате преобразования положение вершин изменится, таким образом, преобразование оставит свой след. Вершины нумеруются исключительно из соображений удобства.

Первая разновидность движения, которую мы рассмотрим, — поворот на 120° против часовой стрелки относительно центра треугольника.

Обозначим это преобразование через R. Как я уже говорил, увидеть результат R нельзя, но если мы бы, к примеру, пронумеровали вершины треугольника, начиная с верхней, против часовой стрелки, то можно было бы сказать, что R переводит первую вершину в третью, вторую — в первую, третью — во вторую. Проще всего показать это на рисунке.

43

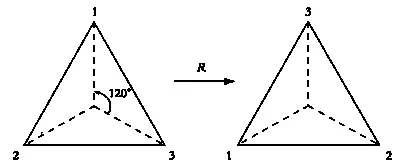
Результат поворота R.

Видите? Треугольник не изменился, но теперь его вершины пронумерованы 3—1—2, а не 1—2—3.

R не единственное преобразование, оставляющее треугольник неизменным.

Представьте себе осевую симметрию, ось которой пересекает треугольник. Чтобы в результате симметрии треугольник остался неизменным, нужно внимательно выбрать ось, так как при некоторых видах симметрии положение треугольника изменится.

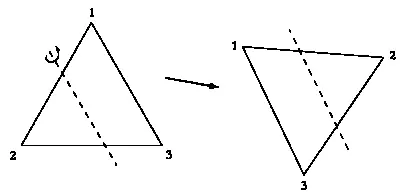
Симметрия, при которой треугольник меняется.

Треугольник останется неизменным, если ось симметрии проходит через его центр и одну из вершин. Поворот мы обозначили через R, симметрию — через S. Та же схема, которой мы проиллюстрировали поворот R, поможет показать, как изменится положение вершин при симметрии S. Первая вершина останется на месте, а вторая и третья поменяются местами. Теперь вершины пронумерованы не 1—2—3, а 1-3-2.