Стюарт Исакофф - Музыкальный строй. Как музыка превратилась в поле битвы величайших умов западной цивилизации

Интерес Галилея к экспериментальным наблюдениям – в том числе, скорее всего, конкретно к маятникам – он унаследовал от своего отца, музыканта с научным складом ума по имени Винченцо, который, по всем свидетельствам, был человеком не менее пылким и упрямым, чем его сын. В самом деле, акустические эксперименты Винченцо Галилея – в том числе тот, в котором он использовал подвесы (статичные маятники) для изменения натяжения струн – привели к одному из самых громких скандалов в истории музыки.

Все началось с учебы. Винченцо с компанией других музыкантов, поэтов и аристократов регулярно встречались в доме влиятельного и колоритного флорентийского графа Джованни Барди, чтобы сочинять музыку и беседовать на темы искусства, науки и философии. Их группа, известная как “Флорентийская камерата”, была колыбелью интеллектуальной деятельности – “фактически замечательной бессрочной академией”, как отозвался о ней позже сын Барди Пьетро (отметив также для потомков, что ее члены “держались от пороков и особенно любого рода азартных игр на расстоянии”).

Барди был центром притяжения этого кружка – настоящим человеком Возрождения. Он участвовал в покорении Сиены, сражался против турок на Мальте и командовал тосканским войском, защищавшим императора Максимилиана II в Венгрии. При этом мог он и сымпровизировать сонет. Когда в 1574 году его принимали в Академию дельи Альтерати, то отмечали блестящее знание математики, астрологии, космографии и поэзии. “Поэтому неудивительно, – писал его анонимный покровитель, – что этот человек, прекрасный и душой, и телом, всегда испытывал острое влечение к восхитительной гармонии музыки, искусства древних греков, среди которых благородные занятия и добродетели процветали настолько, что любой, кто не был им обучен, считался человеком никчемным и недостойным”.

Как и многие его коллеги, Барди относился к разного рода искусствам с серьезностью, подобающей той роли, которую отводили им в деле возрождения цивилизации. В вопросах культуры его отличал тот же пыл, который он демонстрировал против турок на поле боя, – немудрено, что его не обошел стороной и самый важный спор той эпохи: кто был первым поэтом, Ариосто или Тассо? (Если кто-то ведет счет, Барди голосовал за Ариосто.) До того как политическая удача изменила ему (граф поддержал свадьбу Франческо Медичи и Бьянки Капелло, чем прогневал Фердинандо Медичи, и тот, взойдя на престол в 1587 году, передал многие его привилегии при дворе – в частности, управление зрелищами и развлечениями – римлянину Эмилио де Кавальєри), Барди был бесстрашным возмутителем спокойствия в художественной жизни Флоренции. Однако когда он принял решение отправить Винченцо Галилея в Венецию, в обучение к прославленному теоретику музыки Джозеффо Царлино, он и подумать не мог, каким политическим скандалом это окончится.

Царлино был выдающимся музыкантом, знатоком логики, греческого и иврита – его, кроме того, рукоположили в духовный сан. Он родился в 1517 году в Кьодже, на одном из островов в венецианской лагуне, и обучался поначалу у местных францисканских монахов, после чего стал учеником знаменитого композитора Адриана Вилларта. Его книга “Основы гармоники” 1558 года стала важной вехой в истории музыкальной науки – это всеобъемлющий трактат о философских, математических и практических сторонах композиции, охватывающий историю искусства гармонии во всей ее полноте: от Древней Греции до современности.

На ее страницах автор поднимал, в числе прочего, один щекотливый вопрос. Царлино верил, что музыка – это сила, которая помогает найти равновесие между душой и телом, а также связать друг с другом далекие части света, потому что ее система зиждется на гармонических пропорциях, то есть соотношениях, открытых Пифагором. Однако пифагоровы формулы не учитывали некие созвучия, вошедшие в моду в эпоху Возрождения – большие и малые терции, а также их зеркальные отображения – сексты. Как же заделать эту брешь между теорией и практикой?

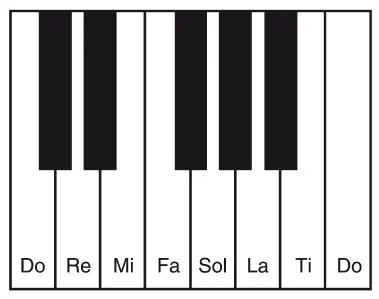
Царлино спас Пифагора, отредактировав его учение. Согласно античному канону, октава (от одного до до следующего) образуется в соотношении 2:1, квинта (от до до соль) в соотношении 3:2, а кварта (от до до фа) в соотношении 4:3. Для Пифагора доказательством совершенства этих музыкальных формул было то, что в них используются лишь первые четыре целых числа (при сложении 1, 2, 3 и 4 дают волшебное число 10 – по Пифагору, символ полноты и завершенности). Однако использование лишь первых четырех целых чисел не позволяет образовать большую терцию (от до до ми) с соотношением 5:4, большую сексту (от до до ля) с соотношением 5:3 и малую терцию (от ре до фа) с соотношением 6:5.