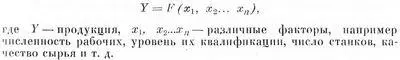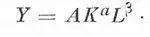Андрей Аникин - Юность науки. Жизнь и идеи мыслителей-экономистов до Маркса

Данной цели, скажем увеличения сбора пшеницы на 50 %, можно достичь разными путями: расширением посевных площадей или увеличением прилагаемого труда и материальных затрат (капитала) на тех же площадях, приложением дополнительного капитала при данном количестве труда или добавлением труда. Конечно, в реальной жизни задача будет решаться путем комбинации прироста элементов (факторов). Но в каких пропорциях их лучше комбинировать? Как следует учесть конкретное положение в данной стране или районе, в особенности степень дефицитности каждого вида ресурсов? Если есть большие свободные площади — одно дело. Если их нет, но есть масса незанятых рабочих рук, — другое. И так далее. Ясно, что все это важные вопросы, которые ставит жизнь перед экономической наукой. Они могут вставать как в масштабе отдельного предприятия (в микроэкономическом плане), так и в масштабе страны (в макроэкономическом плане).

Национальный доход или общественный продукт страны можно рассматривать как массу производимых за год потребительных стоимостей. Денежная оценка этих величин представляет собой способ измерения единой мерой физического объема всей этой бесконечно многообразной совокупности: цемента и штанов, автомобилей и сахара… Изменения их отражают прирост физического объема продукции, т. е. прирост богатства, благосостояния. При такой трактовке вполне обоснован вопрос о доле национального дохода (или продукта), приходящейся на каждый из факторов, участвующих в производстве, и о доле прироста этих величин, даваемой приростом каждого из факторов. Исследование функциональных зависимостей между затратами факторов имеет важное значение для повышения эффективности народного хозяйства. Конечно, предположения о независимости каждого из факторов в создании продукции (рассматриваемой как сумма потребительных стоимостей), о делимости этих факторов и т. д. являются упрощенными допущениями. Но, помня об этих допущениях и учитывая ограничения, налагаемые на анализ действительными условиями, мы можем с определенным эффектом использовать «факторный» анализ производства. Одним из методов этого анализа, широко применяемым в настоящее время, является метод производственных функций. [167] Исторически возникновение этого метода связано с буржуазно-апологетической теорией распределения, которая восходит к Сэю. Однако в дальнейшем практические нужды капиталистической экономики обусловили его использование для решения конкретных задач технико-экономического характера с помощью математики и статистики. Как замечает советский экономист И. Осадчая, из факта первоначальной связи метода производственных функций с теорией факторов производства как теорией распределения «вовсе не следует, что необходимо отвергнуть и сам аппарат производственных функций, который можно отделить от этой вульгарной основы и при соответствующей научной интерпретации использовать в целях анализа важных аспектов роста производства» (И. М. Осадчая. К оценке основных направлений в теории экономического роста. В кн. «Современный капитализм и буржуазная политическая экономия». М., «Мысль», 1967, стр. 162). В общем виде можно считать, что объем производства (данного товара или ряда товаров, на данном предприятии или в данной стране и т. д.) является функцией ряда переменных, число которых может быть как угодно велико. В математических символах это можно записать:

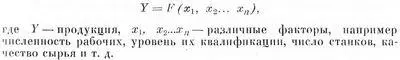
Было предложено множество видов этой функции с различной комбинацией аргументов. Наиболее известной является функция Кобба — Дугласа, названная так по имени американских ученых 20-х годов, и имеющая вид:

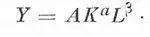
Здесь предполагается, что объем производства определяется двумя факторами: К (количеством капитала, т. е. используемых средств производства) и L (количеством труда). Степенные показатели α и β показывают, на сколько процентов увеличится продукция, если увеличить на 1 % соответственно количество капитала и труда, каждый раз оставляя количество другого фактора фиксированным.

Величина А есть коэффициент пропорциональности; ее можно трактовать также, как величину, учитывающую все качественные, не выражающиеся в количествах капитала и труда, факторы производства.