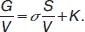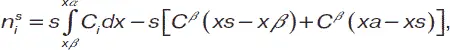Елена Оробейко - Коллоидная химия. Шпаргалка

G = G s + G v = δS + KV.

Разделив это выражение на объем фазы, получаем:

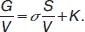
Из последнего уравнения следует, что при неизменном объеме фазы вклад поверхностной энергии в общую энергию фазы возрастает с увеличением удельной поверхности или степени дисперсности фазы. Если степень дисперсности фазы невелика, вкладом поверхностной энергии в полную энергию фазы обычно пренебрегают. Вклад поверхностного слоя в свойства фазы и системы учитывают при изучении дисперсных систем– гетерогенных систем, одна из фаз которых является сплошной (дисперсионная среда),а другая – раздробленной (дисперсная фаза).

На границе конденсированной фазы с газом поверхностное натяжение всегда положительно, поскольку частицы конденсированной фазы взаимодействуют друг с другом сильнее, чем с молекулами газа. Конденсированная фаза будет стремиться уменьшить свою поверхностную энергию, уменьшая либо площадь поверхности фазы (поэтому капля жидкости в невесомости принимает форму сферы), либо поверхностное натяжение. Процесс самопроизвольного изменения концентрации вещества у поверхности раздела двух фаз называется адсорбцией.

Разделяющая поверхность– это геометрическая поверхность, которая воспроизводит форму поверхности разрыва и располагается параллельно последней. Если представить идеализированную систему в которой каждая из интенсивных величин имеет характерные для данной объемной фазы значения, и сравнить ее с реальной системой, то получим, что разности соответствующих экстенсивных параметров в данных системах представляют собой поверхностные избытки. Например, состав поверхностного слоя определяется избыточным числом молей компонентов n i s .

Для нахождения последнего необходимо рассмотреть изменение концентрации компонента системы вдоль нормали, направленной из одной фазы в другую. В реальных системах данное изменение выражается функцией С ( x ), которая представляет собой кривую и имеет постоянные величины в глубине фаз. В идеализированной системе данная функция представлена двумя прямыми, доходящими до разделяющей поверхности. Состав поверхностного слоя будет выражен формулой:

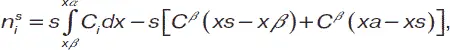
где n i s– избыток количества вещества в поверхностном слое; xb и xa – объемы разделяемых фаз;

C bи C a– концентрация вещества в реальной и идеализированной системах; s – площадь поверхности раздела.

Итак, параметр n i sвыражает избыток компонента, связанный со «сгущением» интенсивного параметра в области поверхностного слоя, – концентрации С . Аналогично в виде избытков выражаются все термодинамические функции поверхностного слоя. Так, энергия поверхностного слоя определяется как разность ее значений в реальной и идеализированной системах:

U s= U – ( U α+ U β)

или

U = U s+ U α+ U β.

Члены правой части этих выражений различаются тем, что U αи U βявляются полными количествами энергии в двух объемных фазах, а U sпредставляет собой поверхностный избыток.

Аналогичные выражения записывают для других термодинамических функций: энтальпии, энтропии свободных энергий Гельмгольца и Гиббса.

Достоинством данного метода описания поверхностного слоя является отсутствие необходимости уточнения его границ. Функции, выражающие избытки, являются инвариантными в отношении толщины поверхностного слоя, однако они зависят от положения разделяющей поверхности.

Поверхностный слой может подвергаться воздействию изменений температуры и состава. Поэтому необходимо принять во внимание в качестве переменных поверхностные энтропию S sи состав n s , в результате будет получено фундаментальное уравнение для энергии разделяющей поверхности:

dU s= T s dS s+ σ ds + Σ μ s dn s,

где dU s– внутренняя энергия поверхностного слоя T s– температура разделяющей поверхности;

S s– энтропия поверхностного слоя; s – коэффициент пропорциональности, численно равный поверхностному натяжению; s – площадь поверхностного слоя; m s– химический потенциал поверхностного слоя; n s– состав поверхностного слоя.