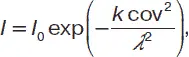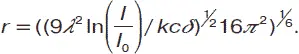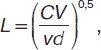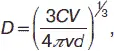Елена Оробейко - Коллоидная химия. Шпаргалка

Дж. Рэлеем был рассмотрен простейший случай рассеяния света при следующих условиях:

1) малой концентрации дисперсной системы;

2) малом размере частиц (отношение длины волны падающего света formula к радиусу частицы r не менее 10);

3) изометричной форме частиц.

Уравнение Рэлея справедливо для монодисперсных разбавленных коллоидных растворов при размерах частиц дисперсной фазы r < 40–70 нм. Более общие выводы о рассеянии света, справедливые для систем всех степеней дисперсности, сформулированы в теории Г. Ми . В данной теории учитывается, что при больших размерах частиц картина рассеяния света осложняется возникающими электрическими и магнитными полями. Максимум рассеяния согласно Г. Ми имеет место при размерах частиц около 0,25 λ , где λ – длина волны видимой части спектра.

Явления рассеяния и поглощения света связаны также с такими свойствами, как окраска растворов, концентрация растворенного вещества. Поглощение света имеет избирательный характер. Поглощение света для молекулярных растворов определяется по уравнению Бугера-Ламберта-Бера:

I = I 0e — kcδ,

где I и I 0 – интенсивность падающего света и света, прошедшего через раствор; k – коэффициент поглощения, зависящий от природы растворенного вещества и длины волны; c – концентрация поглощенного вещества; d – толщина слоя раствора.

Из данного уравнения можно вывести соответствующие уравнения для определения относительной прозрачности и относительного поглощения:

I / I 0= e — kcδ;

( I 0– I ) / I 0= 1 – e — kcδ.

Для коллоидных растворов в уравнение Бугера-Ламберта-Бера вносят поправку, которая необходима для учета рассеяния света. Количество рассеянного света эквивалентно дополнительному количеству поглощенного света. В связи с этим приведем модифицированную формулу, в которой учитывается явление светорассеяния:

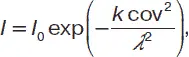
где v – объем коллоидной частицы.

Из последнего уравнения можно вывести формулу для расчета размеров коллоидной частицы. Предположим, что частица имеет правильную сферическую форму.

Тогда радиус этой частицы будет определяться так:

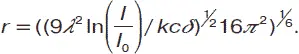
Эмпирически радиус частицы в жидком растворе можно определить методом ультрамикроскопии. Для этого при помощи микрометрической окулярной шкалы выделяют определенный объем коллоидного раствора, в котором визуально подсчитывают количество коллоидных частиц. Если известна масса частицы, то, учитывая плотность диспергированного вещества, можно определить объем и размеры частицы.

Поскольку ультрамикроскоп позволяет косвенно судить о форме коллоидных частиц, то необходимо принять во внимание две формулы. Если форма частицы представляет собой куб, то справедливо, что

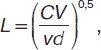
если частица представляет собой сферу, то

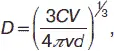
где С – массовая концентрация коллоидного раствора; V – выделенный оптический объем; v – число частиц в объеме V; L – ребро куба; D – диаметр сферы.

Своеобразие дисперсных систем определяется большой удельной поверхностью дисперсной фазы и физико-химическим взаимодействием дисперсной фазы и дисперсионной среды на границе раздела фаз. C повышением дисперсности вещества все большее значение имеют его свойства, определяемые поверхностными явлениями, т. е. совокупностью процессов, происходящих в межфазовой поверхности. Эти свойства обусловлены избытком свободной энергии поверхностного слоя, особенностями его структуры и состава.

Поверхностные явления могут иметь физический характер или сопровождаться химическими превращениями; они протекают на жидких (легкоподвижных) и твердых межфазных границах. Поверхностные явления, связанные с действием поверхностного натяжения и вызываемые искривлением жидких поверхностей раздела, называются также капиллярными явлениями. К ним относятся: