Изменение энтальпии обычно относят для стандартного состояния вещества: т. е. для чистого вещества в определенном (твердом, жидком или газообразном) состоянии, при давлении 1 атм = 101 325 Па, температуре 298 К и концентрации веществ 1 моль/л.
Стандартная энтальпия образования ΔН обр– теплота, выделяемая или поглощаемая при образовании 1 моль вещества из простых веществ, его составляющих, при стандартных условиях. Так, например, ΔН обр (NaCl) = -411 кДж/моль. Это означает, что в реакции Na(тв) + ½Cl 2(г) = NaCl(тв) при образовании 1 моль NaCl выделяется 411 кДж энергии.
Стандартная энтальпия реакции ΔН– изменение энтальпии в ходе химической реакции, определяется по формуле: ΔН= ΔН обр (продуктов) – ΔН обр (реагентов).
Так для реакции NH 3(г) + HCl(г) = NH 4Cl(тв), зная ΔH o 6 p(NH 3)=-46 кДж/моль, ΔH o 6 p(HCl) = -92 кДж/моль и ΔH o 6 p(NH 4Cl) = -315 кДж/моль имеем:
ΔH = ΔH o 6 p(NH 4Cl) – ΔH o 6 p(NH 3) – ΔH o 6 p(HCl) = -315 – (-46) – (-92) = -177 кДж.
Если Δ Н < 0, то реакция экзотермическая. Если Δ Н > 0, то реакция эндотермическая.
ЗаконГесса: стандартная энтальпия реакции зависит от стандартных энтальпий реагентов и продуктов и не зависит от пути протекания реакции.
Самопроизвольно идущие процессы могут быть не только экзотермическими, т. е. процессами с уменьшением энергии ( Δ Н < 0), но могут быть и эндотермическими процессами, т. е. процессами с увеличением энергии ( Δ Н > 0). Во всех этих процессах «беспорядок» системы увеличивается.
Энтропия S – физическая величина, характеризующая степень беспорядка системы. S – стандартная энтропия, ΔS – изменение стандартной энтропии. Если ΔS > 0, беспорядок растет, если AS < 0, то беспорядок системы уменьшается. Для процессов в которых растет число частиц, ΔS > 0. Для процессов, в которых число частиц уменьшается, ΔS < 0. Например, энтропия меняется в ходе реакций:
СаО(тв) + Н 2O(ж) = Са(OH) 2(тв), ΔS < 0;
CaCO 3(тв) = СаО(тв) + CO 2(г), ΔS > 0.
Самопроизвольно идут процессы с выделением энергии, т. е. для которых Δ Н < 0, и с увеличением энтропии, т. е. для которых ΔS > 0. Учет обоих факторов приводит к выражению для энергии Гиббса: G = Н – TS или Δ G = ΔН – Т • ΔS. Реакции, в которых энергия Гиббса уменьшается, т. е. ΔG < 0, могут идти самопроизвольно. Реакции, в ходе которых энергия Гиббса увеличивается, т. е. ΔG > 0, самопроизвольно не идут. Условие ΔG = 0 значит, что между продуктами и реагентами установилось равновесие.
При низкой температуре, когда величина Т близка к нулю, идут лишь экзотермические реакции, так как TΔS – мало и ΔG = Δ Н < 0. При высоких температурах значения TΔS велико, и, пренебрегая величиной Δ Н, имеем ΔG = – TΔS, т. е. самопроизвольно будут идти процессы с увеличением энтропии, для которых ΔS > 0, a ΔG < 0. При этом чем больше по абсолютной величине значение ΔG, тем более полно проходит данный процесс.
Величина AG для той или иной реакции может быть определена по формуле:
ΔG = ΔС обр(продуктов) – ΔG o б p(реагентов).
При этом величины ΔG o бр, а также Δ Н обр и ΔS o брдля большого числа веществ приведены в специальных таблицах.
Скорость химической реакции( v ) определяется изменением молярной концентрации реагирующих веществ в единицу времени:
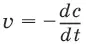
где v – скорость реакции, с – молярная концентрация реагента, t – время.
Скорость химической реакции зависит от природы реагирующих веществ и условий протекания реакции (температуры, концентрации, присутствия катализатора и т. д.)
Влияние концентрации. Вслучае простых реакций скорость реакции пропорциональна произведению концентраций реагирующих веществ, взятых в степенях, равных их стехиометрическим коэффициентам.
Для реакции
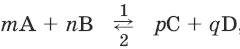
где 1 и 2 соответственно направление прямой и обратной реакции:
v 1= k 1× [А] m × [В] nи
v 2= k 2 × [C] p × [D] q
где v – скорость реакции, k – константа скорости, [А] – молярная концентрация вещества А.
Молекулярность реакции– число молекул, участвующих в элементарном акте реакции. Для простых реакций, например: mA + nB → рС + qD, молекулярность равна сумме коэффициентов (m + n). Реакции могут быть одномолекулярными, двумолекулярными и редко трехмолекулярными. Реакции более высокой молекулярности не встречаются.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

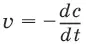
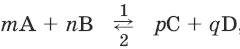







![Кирилл Рябов - Никто не вернётся [сборник litres]](/books/385781/kirill-ryabov-nikto-ne-vernetsya-sbornik-litres-thumb.webp)



