Тибо Дамур - Мир по Эйнштейну. От теории относительности до теории струн

На плоской поверхности, например на лежащем на столе листе бумаги, можно легко определить местоположение точки с помощью обычной прямоугольной сетки, какая используется в школьных тетрадках или на миллиметровой бумаге. Такую регулярную сетку уже невозможно реализовать на поверхности, имеющей всевозможные выпуклости и впадины. Чтобы зафиксировать любую точку на искривленной поверхности, мы, таким образом, используем два параметра, скажем x и y , которые больше не имеют простого смысла длины и ширины. Например, на поверхности Земли в качестве «первой координаты» x можно использовать долготу, а в качестве «второй координаты» y – широту. Следует отметить, что такие координаты можно использовать, даже когда земную поверхность невозможно аппроксимировать сферой: например, на возвышенности или в низине. При этом нет необходимости вводить третью координату (скажем, высоту над уровнем моря), поскольку двух первых координат (долготы и широты) будет достаточно, чтобы определить положение на Земле, а высота будет определяться некоторой функцией долготы и широты. Отсюда легко видеть, что если использовать сетку, определяемую долготой и широтой, на небольшой части поверхности Земли на склоне горы или ущелья, то эта сетка будет представлять собой деформацию привычной сетки из школьной тетрадки в клетку: поверхность по-прежнему будет разбиваться на ячейки двумя семействами линий, но каждая ячейка будет не квадратом, а чем-то вроде параллелограмма, точнее, ее стороны просто не будут равны друг другу и перестанут пересекаться под прямым углом.

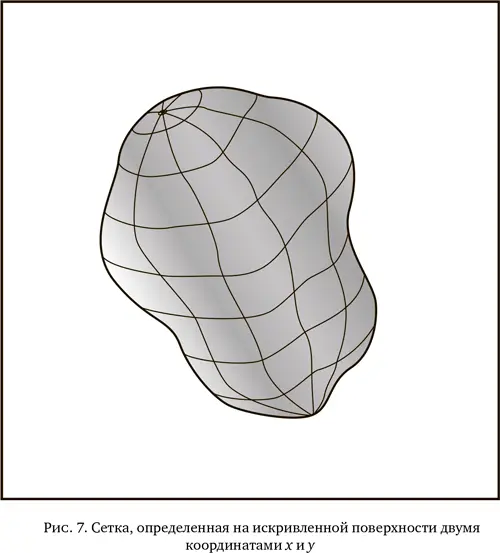
Итак, локально можно сопоставить каждый небольшой фрагмент получившегося разбиения на ячейки с обычным разбиением на параллелограммы, сделанном на касательной плоскости. Обобщение теоремы Пифагора применительно к непрямоугольным треугольникам говорит нам, что квадрат расстояния между двумя узлами такой (плоской) сетки дается суммой квадратов разностей координат между двумя узлами и их удвоенным произведением. Чтобы определить квадрат расстояния между близкими точками вообще любой искривленной поверхности, точки которой фиксируются двумя координатами x и y , необходимо, таким образом, задать в каждой точке три величины: коэффициент перед квадратом dx ² разности dx между первыми координатами двух точек, коэффициент перед квадратом dy ² разности dy между вторыми координатами и коэффициент перед удвоенным произведением 2 dxdy . [Мы рассматриваем математический предел, в котором точки бесконечно близки, отсюда символ d , обозначающий бесконечно малую разность.] Эти три коэффициента определяют геометрию (geometry) рассматриваемой поверхности и по этой причине обозначаются соответственно как g xx, g yy и g xy , где буква g напоминает нам, что речь идет о геометрии.

Во времена обучения в Цюрихском политехническом Эйнштейн высоко ценил курс Карла Фридриха Гёйзера, посвященный «инфинитезимальной геометрии» поверхностей. Гёйзер читал лекции по теории, разработанной знаменитым математиком Карлом Фридрихом Гауссом и фактически изучающей тот самый квадрат расстояния между бесконечно близкими точками, про который мы только что говорили. В связи с этим в 1912 г. Эйнштейн вспомнил, что геометрия «деформированной» (или неплоской) поверхности определяется с помощью трех величин g xx, g yy, g xy , заданных в каждой точке поверхности. Этот набор данных, определяющий для каждой точки поверхности значения трех величин g xx, g yy, g xy , называется «геометрическим тензором», а точнее, «метрическим тензором» g . Эйнштейн понял, что ему требуется обобщение этого понятия на случай, когда (двумерная) поверхность заменяется на (четырехмерное) пространство-время. Математик Бернхард Риман, студент Гаусса, уже обобщил теорию Гаусса для деформированных пространств произвольных размерностей. Однако Риман рассматривал исключительно случай пространств, которые локально, т. е. в окрестности каждой точки, напоминают обычное евклидово пространство. Другими словами, он изучал пространства, в которых геометрическое место точек, разделенных с данной центральной точкой малым значением квадрата расстояния ε², имеет форму деформированной (гипер)сферы, т. е. представляет своего рода «мяч для регби» {68}. Эйнштейн понял, что ему требуется обобщить теорию Римана на случай, когда геометрическое место точек, разделенных с данной центральной точкой малым (положительным) значением квадрата интервала ε², имеет форму деформированных песочных часов {69}.