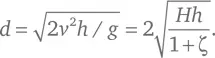
Галилей не упоминал поправку на вращательное движение, выражаемую коэффициентом ζ, но он мог подозревать, что наличие такой поправки уменьшает горизонтальное расстояние, которое преодолевает шар, поскольку он не стал сравнивать это расстояние с величиной d = √( Hh ), которую можно было бы ожидать, не учитывая ζ, а лишь проверял тот факт, что для фиксированной высоты стола h пройденное расстояние d было действительно пропорционально √( H) с точностью до нескольких процентов. По каким-то причинам Галилей так ни разу и не опубликовал результаты этого эксперимента.
Для множества задач в астрономии и математике удобно представлять параболу как предельный частный случай эллипса, один фокус которого находится очень далеко от другого. Как демонстрировалось в техническом замечании 18, уравнение эллипса с большой осью 2 a и малой осью 2 b таково:
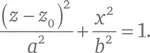
В нем мы для удобства выполнения дальнейшего анализа заменили координаты x и у , которые использовали в техническом замечании 18, на z – z 0и x , соответственно, где z 0 – произвольно выбираемая константа. Центр этого эллипса находится в точке с координатами z = z 0и x = 0. Как мы видели в замечании 18, фокус эллипса находится в точке z – z 0= − ae, x = 0, где e – эксцентриситет, определяемый как e ² ≡ 1 − b ²/ a ², а точка, в которой кривая находится ближе всего к этому фокусу, расположена в z − z 0= − a и x = 0. Удобнее обозначить именно эту точку наибольшего сближения с фокусом координатами z = 0 и x = 0, выбрав значение z 0равным a , и в этом случае ближайший фокус окажется расположен от нее на расстоянии z = z 0 – ea = (1 – e ) a . Теперь мы хотим сделать a и b бесконечно большими, так что противоположный фокус эллипса удалится в бесконечность и у нашей кривой не будет определенной максимальной координаты x , но при этом нужно, чтобы расстояние между фокусом и точкой наиболее тесного сближения с кривой (1– e ) a оставалось бы конечным, так что мы задаем:
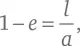
где l остается постоянной, в то время как a стремится к бесконечности. Так как e здесь предельно приближается к единице, малая полуось будет выражаться как:
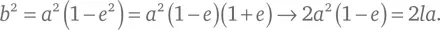
Принимая, что z 0= a , и используя эту формулу для b ², приведем уравнение эллипса к следующему виду:
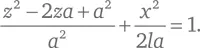
Из левой части вычитаем слагаемое a ²/ a ², а из правой – равную ему единицу. Затем обе части умножаем на a и получаем:
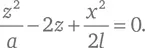
В случае, когда a значительно больше x, y или l , можно опустить первый член, и уравнение приходит к виду:
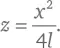
Это то же самое уравнение, которое мы выше вывели для описания движения горизонтально выстреливаемой пули, если мы примем, что:
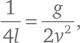
так что фокус параболы F находится на расстоянии l = v ²/2 g ниже начальной позиции пули (см. рис. 19).
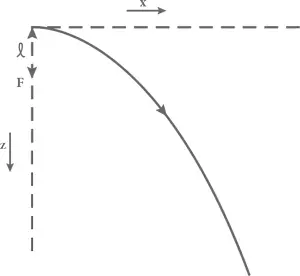
Рис. 19. Параболическая траектория пули, которой стреляют горизонтально с возвышенности.Точка F – фокус параболы.
Параболы, как и эллипсы, можно рассматривать как конические сечения, но в случае параболы плоскость, которой рассекается конус, параллельна поверхности конуса. Принимая, что уравнение конуса, центральная ось которого совпадает с осью z , имеет вид √( x ² + y ²) = α ( z − z 0), а уравнение плоскости, параллельной данному конусу, просто y = α ( z − z 0), где z 0 – произвольная константа, кривая пересечения конуса и плоскости удовлетворяет равенству:
Читать дальше
Конец ознакомительного отрывка
Купить книгу

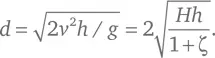
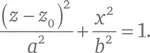
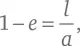
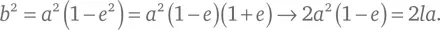
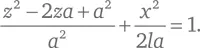
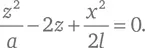
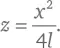
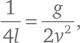







![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)



