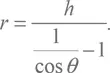
К примеру, наблюдая горизонт на горе в Индии, аль-Бируни нашел, что θ = 34’. Косинус этого угла cos θ = 0,999951092, а 1/cos θ – 1 = 0,0000489. Значит,
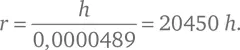
Согласно аль-Бируни, высота этой горы составляла 652,055 локтя (это число дано с точностью, намного превышающей доступную ему точность измерений), что дает результат r = 13,3 млн локтей, хотя он сам приводит число 12,8 млн локтей. В чем именно аль-Бируни ошибся, мне неизвестно.
17. Геометрическое доказательство теоремы о средней скорости
Построим график изменения скорости в зависимости от времени для движения с постоянным ускорением, отложив скорость вдоль вертикальной оси, а время – вдоль горизонтальной. График будет представлять собой прямую линию от нуля до конечной скорости в конечный момент времени. В каждый достаточно малый отрезок времени пройденное расстояние равняется произведению скорости, которое имело тело в этот момент (примем, что изменение скорости пренебрежимо мало в этот промежуток времени, если он сам мал), на длину временно́го отрезка.
Таким образом, пройденное расстояние равно площади узкого прямоугольника, высота которого равна высоте графика скорости в этот момент времени, а ширина отмечает достаточно малый отрезок времени (см. рис. 11а). Такими прямоугольниками можно заполнить всю область под графиком от начального до конечного момента времени, и полное пройденное расстояние в этом случае будет равняться сумме их площадей, то есть площади области под графиком (см. рис. 11б).
Конечно, какими бы узкими мы ни делали эти прямоугольники, можно лишь приближенно говорить, что площадь области под графиком равна сумме их площадей. Но если мы будем делать их все более и более узкими, мы будем получать все более и более близкий к истинному результат. Представляя себе бесконечное количество бесконечно тонких прямоугольников разбиения, мы можем заключить, что пройденное телом расстояние численно равно площади, заключенной под графиком.
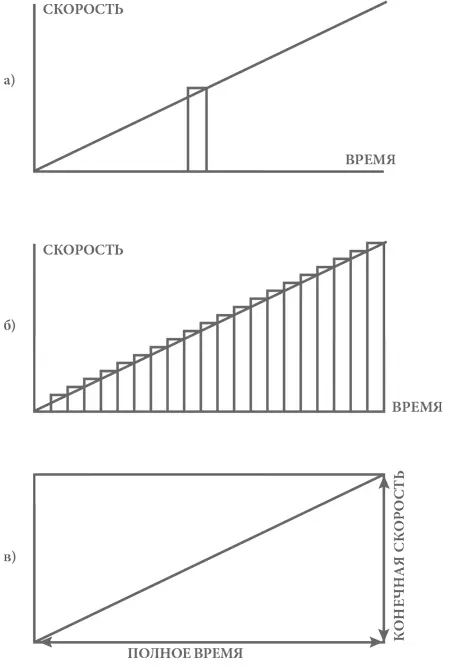
Рис. 11. Геометрическое доказательство теоремы о средней скорости.Наклонная линия – это график скорости в зависимости от времени для равномерно ускоряющегося тела, первоначально находившегося в состоянии покоя: а) ширина узкого прямоугольника соответствует малому отрезку времени. Его площадь примерно равна расстоянию, пройденному за этот промежуток времени; б) весь период времени равноускоренного движения разбивается на малые промежутки. По мере увеличения количества промежутков сумма площадей построенных на них прямоугольников все точнее приближается к площади области под наклонным графиком; в) площадь под наклонным графиком скорости равна половине произведения конечной скорости на полное время ускоренного движения.
Суть рассуждения не изменится и в том случае, если ускорение не будет постоянным и график скорости не будет прямолинейным. Оказывается, мы только что вывели основополагающий принцип интегрального исчисления: если взять график изменения во времени некоторой величины, то ее суммарное изменение в пределах какого-то промежутка времени будет равно площади, заключенной под графиком этой кривой, в пределах того же промежутка. Но в случае равномерного изменения величины, как для нашего постоянного ускорения, эту площадь можно найти простейшим геометрическим расчетом по следующей теореме: площадь прямоугольного треугольника равна половине произведения длин его катетов, то есть двух его сторон, не являющихся гипотенузой. Это очевидно из того факта, что, сложив два одинаковых прямоугольных треугольника вместе, мы получим прямоугольник, площадь которого равна произведению длин двух его сторон (см. рис. 11в). В нашем случае катетами являются конечная скорость и полное время ускоренного движения. Пройденное расстояние равно площади прямоугольного треугольника таких размеров, то есть половине произведения конечной скорости на полное время. Но, поскольку скорость возрастает от нуля в постоянном темпе, ее среднее значение равно половине его конечного значения, поэтому пройденное телом расстояние равно произведению средней скорости на полное время. Это и есть теорема о средней скорости.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

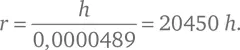







![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)



