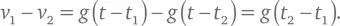
Несмотря на то что и v 1, и v 2растут со временем, их разность не зависит от конкретного момента t , поэтому расстояние s между двумя каплями просто увеличивается прямо пропорционально времени:
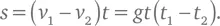
Например, если вторая капля срывается со среза сливного лотка на одну десятую долю секунды позже первой, то половину секунды спустя две капли окажутся на расстоянии 9,8 × 1/2 × 1/10 = 0,49 м одна от другой.
Открытие закона отражения световых лучей Героном Александрийским явилось одним из самых ранних примеров того, как закон физики выводится средствами математики из другого, более общего принципа. Допустим, наблюдатель в точке A видит отражение в зеркале объекта в точке B . Если наблюдатель видит изображение в точке P на зеркале, то световой луч в таком случае проделал путь из точки B в точку P , а затем в точку A (Герон, вероятно, сказал бы, что луч прошел от наблюдателя из точки A к зеркалу, а затем к объекту в точке B , как если бы глаз таким образом дотронулся до объекта, но на ход наших рассуждений это не повлияет). Задача заключается в следующем: где именно на зеркале находится точка P ?
Чтобы ответить на этот вопрос, Герон предположил, что свет всегда следует кратчайшим путем. В случае отражения это означает, что точка P должна быть расположена так, чтобы общая длина пути из B в P , а затем в A была бы наименьшей среди всех возможных путей из двух прямолинейных отрезков между точкой B , зеркалом и точкой A . Отсюда он заключил, что угол θ п (тета п ) между зеркалом и падающим на него лучом света (отрезком между точкой B и зеркалом) равен углу θ о между зеркалом и отраженным лучом (отрезком между зеркалом и точкой A ).
Доказательство правила о равных углах падения и отражения таково. Начертим прямую, перпендикулярную поверхности зеркала, проходящую через точку B и точку B ′, которая находится на таком же расстоянии позади зеркала, как B перед ним (см. рис. 3). Допустим, что эта прямая пересекает зеркало в точке C . Катеты B ′ C и CP прямоугольного треугольника B ′ CP имеют ту же длину, что и катеты BC и CP в треугольнике BCP , поэтому гипотенузы B ′ P и BP этих двух прямоугольных треугольников также должны быть равны. Значит, полное расстояние, которое луч света проходит из B в P , а потом в A , такое же, как если бы он проходил из B ′ в P , а затем в A . Кратчайшее расстояние между точками B ′ и A – это отрезок прямой, а значит, кратчайший путь между реальным объектом и наблюдателем – такой, при котором точка P лежит на отрезке B ′ A . В случае пересечения двух прямых линий противолежащие по отношению к точке пересечения углы равны, поэтому угол θ между отрезком B ′ P и зеркалом равен углу θ о между отраженным лучом и зеркалом. Но поскольку у прямоугольных треугольников B ′ CP и BCP все стороны одинаковы, угол θ должен быть также равен углу θ п между падающим лучом и зеркалом. Таким образом, поскольку и θ о , и θ п равны θ, они взаимно равны. Это фундаментальное правило равенства углов падения и отражения определяет положение точки P , которая соответствует изображению объекта в зеркале.
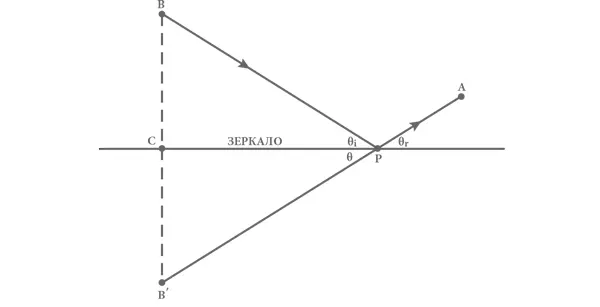
Рис. 3. Доказательство теоремы Герона.Теорема доказывает, что кратчайший путь из объекта B до поверхности зеркала и затем к наблюдателю в точке A таков, что углы θ п и θ о равны. Начерченные сплошной линией отрезки помечены стрелками, показывающими направление движения луча света. Штриховая линия – перпендикуляр к поверхности зеркала между точкам B и B’ , находящимися на одинаковом расстоянии от зеркала, но по разные стороны от него.
9. Плавающие и погруженные в жидкость тела
В своем великом труде «О плавающих телах» Архимед предположил, что если различные тела плавают или иным образом удерживаются в воде так, что одинаковые сечения на одинаковых глубинах прижимаются вниз различным весом, то и вода, и тела придут в движение и успокоятся тогда, когда все сечения на всех глубинах окажутся придавлены одинаковым весом. Исходя из этого предположения, он сделал несколько общих выводов о поведении плавающих и погруженных тел, некоторые из них даже имели важное практическое значение.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

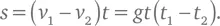







![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)



