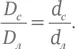
Исходя из результатов наблюдения 1, Аристарх получил значение отношения D с / D л = 19,11, в то время как настоящее соотношение диаметров двух тел близко к 390.
Тень Земли в месте расположения Луны во время лунного затмения широка настолько, что может точно вместить сферу диаметром в два раза больше Луны.
Обозначим P точку, где находится вершина конуса тени, отбрасываемой Землей. У нас получается три подобных треугольника: треугольник, образованный поперечным диаметром Солнца и линиями между его концами и точкой P; треугольник, образованный поперечным диаметром Земли и линиями между его концами и точкой P ; и треугольник, образованный двойным поперечным диаметром Луны и линиями между его концами и точкой P (см. рис. 5в). Следовательно, соотношения подобных сторон во всех этих треугольниках взаимно равны. Предположим, что точка P находится на расстоянии d 0 позади Луны. Тогда расстояние между этой точкой и Солнцем составляет d с + + d л + d 0 , а между ней же и Землей – d л + d 0 , поэтому
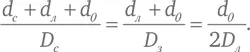
Выполнив несложные алгебраические преобразования, мы можем найти из второго равенства выражение для d 0 :
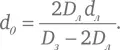
Подставляя его в первое равенство и перемножая обе части на D зD с ( D з – 2 D л ), получаем:
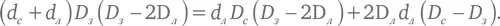
Слагаемые d лD с × (−2 D л ) в левой части и 2 D лd лD с в правой части взаимно обращаются в 0. Оставшиеся в правой части слагаемые имеют общий множитель D з , который сокращается с множителем D з в левой части. Таким образом, у нас получается формула для D з :
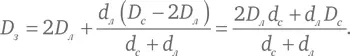
Зная результат наблюдения 2, то есть выведенное нами равенство d с / d л = D с / D л , уравнение выше может быть записано с использованием одних лишь диаметров небесных тел:
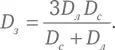
Если мы используем полученное ранее численное значение D с / D л = 19,1, это даст D з / D л = 2,85. Аристарх выразил значение этого отношения как лежащее между 108/43 = 2,51 и 60/19 = 3,16, и число 2,85 замечательно попадает в этот промежуток. Но его настоящее значение равно 3,67. Причина того, что результат Аристарха оказался довольно близок к истинной величине, несмотря на сильную ошибку в оценке отношения D с / D л , в том, что результат вычисления малочувствителен к точному значению D с , если D с много больше D л . В самом деле, если мы совсем выкинем из знаменателя слагаемое D л как ничтожно малое по сравнению с D с , то D с в числителе и знаменателе сократятся, и у нас получится просто D з = 3 D л , что не так уж далеко от истины.
Но значительно более важное историческое значение имел тот факт, что, совмещая значения отношений D с / D л = 19,1 и D з / D л = 2,85, легко найти, что D с / D з = 19,1/2,85 = 6,70. И хотя по-настоящему D с / D з = 109,1, уже и такой результат показывал, что Солнце значительно больше Земли. Аристарх усилил эффект, показав сравнение соотношения не диаметров, а объемов двух тел: если соотношение их диаметров равно 6,7, то соотношение их объемов будет равняться 6,73 = 301. Именно это сопоставление, если верить Архимеду, привело Аристарха к мысли, что Земля обращается вокруг Солнца, а не Солнце вокруг Земли.
Уже описанные нами выкладки Аристарха дают значения всех соотношений диаметров Солнца, Луны и Земли, а также значение отношения расстояний до Солнца и Луны. Однако пока мы никак не можем связать соотношением какой-либо диаметр тела с расстоянием между телами. Это становится возможно при учете результата четвертого наблюдения:
Луна имеет угловой размер 2°.
Поскольку угловой размер дуги полной окружности равен 360° (см. рис. 5 г) и длина окружности радиусом dл равна 2 πdл , то диаметр Луны равен
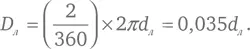
По Аристарху, значение отношения D л / d л лежит в промежутке между 2/45 = 0,044 и 1/30 = 0,033. По неизвестным причинам в сохранившихся трудах Аристарх грубо ошибается в своей оценке видимого углового диаметра Луны. На самом деле он составляет 0,519°, что сводит значение D л / d л к 0,0090. Как мы отметили в главе 8, Архимед в своем труде «Исчисление песчинок» дает величину для углового диаметра Луны 0,5°, что довольно близко к истинному значению и могло бы дать правильные оценки диаметра Луны и расстояния до нее.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

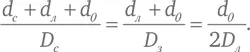
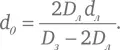
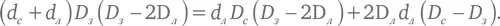
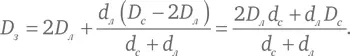
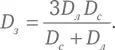
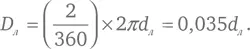






![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)



