Брайан Кокс - Почему Е=mc²? И почему это должно нас волновать

Итак, мы только что завершили очень тонкие рассуждения. Это, конечно, не означает, что мы были правы, принимая исходную гипотезу о наличии «инвариантного» расстояния в пространстве-времени, которое будет справедливо для всех наблюдателей. Но это означает, что наша гипотеза прошла важную проверку на подчинение требованиям принципа причинности. Мы еще не закончили, потому что не просто играем с математикой. Мы физики и пытаемся построить теорию, описывающую устройство нашего мира. Конечным и решающим ее испытанием будет ее способность делать прогнозы, согласующиеся с результатами экспериментов. Но пока мы к этому не готовы, поскольку не знаем, чему равна калибровочная скорость c . Без чисел мы просто не в состоянии ничего вычислить.

Помните: для того чтобы описать понятие расстояния в пространстве-времени, нам нужно значение c , потому что измерять пространство и время необходимо в одних и тех же единицах. Пока мы не можем точно сказать, что собой представляет скорость c . Есть ли в ней что-то интересное? Ключ к ответу лежит в интригующем свойстве только что построенного пространства-времени Минковского. Эти пунктирные линии под углом 45 градусов к осям очень важны. На рис. 7 мы изобразили несколько других кривых, каждая из которых обладает свойством эквидистантности от O в пространстве-времени. Важный момент: мы можем изобразить четыре типа кривых. Одна находится полностью в будущем относительно O , другая – в прошлом, а две оставшиеся расположены слева и справа. Они внушают некоторую тревогу, поскольку пересекают горизонтальную ось так же, как и окружность, когда мы рассматривали формулу Пифагора со знаком плюс. Тогда нам пришлось отвергнуть гипотезу из-за нарушения принципа причинности. Не оказались ли мы в том же тупике в версии со знаком минус? Нет, потому что на сей раз из тупика есть выход. На рис. 7 показано событие B , расположенное в проблемной области; оно находится в прошлом по отношению к событию O . Однако эквидистантная гипербола, все точки которой размещены на одном и том же расстоянии от O в пространстве-времени, пересекает ось пространства. Это говорит о том, что могут быть как наблюдатели, для которых событие B находится по отношению к событию O в будущем, так и наблюдатели, для которых событие B находится по отношению к событию O в прошлом. Не забывайте: для всех наблюдателей расстояние между событиями в пространстве-времени одинаково, даже если по отдельности расстояние в пространстве и расстояние во времени для них различно. Хотя это выглядит как нарушение принципа причинности, к счастью, это совершенно не так.

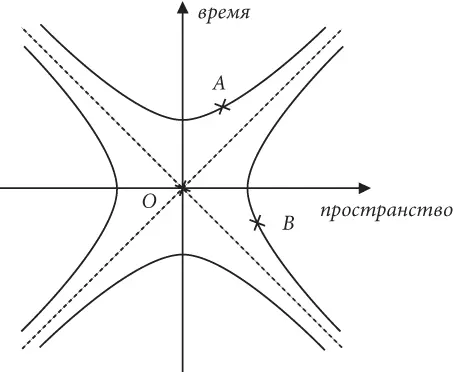
Рис. 7

Как же восстановить принцип причинности в нашей теории пространства-времени? Чтобы ответить на этот вопрос, мы должны более серьезно поразмышлять о том, что мы понимаем под причинностью. Следующая часть рассуждений будет включать космические корабли и лазеры, так что вы сможете немного отдохнуть от иссушающих мозг абстрактных понятий. Давайте вернемся еще раз к событию O – утреннему подъему. А если точнее, сопоставим это событие с моментом, когда перестает звонить будильник. Незадолго до этого с одной из планет системы Альфы Центавра, ближайшей к Земле звездной системы, находящейся на расстоянии четырех световых лет, взлетел космический корабль и направился к Земле. Должны ли все наблюдатели согласиться, что корабль стартовал до того, как я проснулся? С точки зрения принципа причинности все зависит от того, насколько быстро может распространяться информация. Если информация может путешествовать с бесконечной скоростью, то инопланетный корабль теоретически способен выпустить лазерный луч, который мгновенно достигнет Земли и уничтожит мой будильник. В результате я просплю и останусь без завтрака. Это, конечно, ужасно, но поскольку мы ставим мысленный эксперимент, давайте отвлечемся от эмоциональных последствий уничтожения моего будильника и продолжим рассуждать. Выстрел боевого лазера лишает меня завтрака, а значит, порядок этих событий не может быть изменен без нарушения принципа причинности. Это легко увидеть, так как, если бы некий наблюдатель мог прийти к выводу, что выстрел состоялся после моего пробуждения, получилось бы противоречие: я не мог бы проспать просто потому, что уже встал. Мы вынуждены сделать следующее заключение: если информация может переноситься с произвольно высокой скоростью, то порядок любых двух событий никогда не может быть изменен без нарушения закона причины и следствия. Однако в наших рассуждениях есть лазейка, которая позволяет менять порядок определенных пар событий на обратный, но только если они находятся вне 45-градусных прямых. Эти прямые действительно начинают выглядеть очень важными.