Брайан Кокс - Почему Е=mc²? И почему это должно нас волновать

Для того чтобы решить вопрос с плюсом или минусом, следует обратить внимание на принцип причинности. Давайте предположим, что уравнение Пифагора применимо и к расстояниям в пространстве-времени, то есть что s ² = ( ct )² + x ². Теперь еще раз вернемся к нашим событиям – подъему в семь утра и завершению завтрака в восемь – и сделаем нечто такое, от чего у вас побегут мурашки по коже, когда вы вспомните, как сидели на уроках математики в школе и смотрели через окно на футбольное поле, нетронутое и зовущее в солнечный весенний день, – назовем момент пробуждения O , а завершение завтрака – A . Мы делаем это исключительно из соображений краткости, чтобы не описывать каждый раз подробно эти события.

Мы знаем, что пространственное расстояние между O и A равно x = 10 метров, а временн о е – t = 1 час, если x и t измеряю я. Мы еще не решили, чему равно c , но когда будем знать эту величину, то сможем вычислить и расстояние s в пространстве-времени между событиями O и A . Наша гипотеза заключается в том, что, если кто-то пролетит мимо со скоростью, близкой к скорости света, и выполнит те же измерения, расстояние s останется тем же. Иными словами, x и t для этого наблюдателя могут быть (и будут) другими, но они изменятся таким образом, что значение s останется прежним. Рискуя показаться слишком настойчивыми в подчеркивании важности этой мысли, хотим вам напомнить, что наша цель – всегда строить законы физики с использованием инвариантных объектов в пространстве-времени. Расстояние s – именно такой объект. Если это звучит слишком абстрактно, можем повторить сказанное с меньшим количеством математических терминов: правила природы должны выражать соотношения между реальными вещами, а эти вещи находятся в пространстве-времени. Вещь в пространстве-времени сродни объекту, расположенному в комнате. Пространство-время (или комната) представляет собой арену, на которой живет эта вещь. Природа реальных вещей не зависит от точки зрения и мнения наблюдателя, и в этом смысле мы говорим, что она инвариантна. Трехмерным примером чего-то, что не является инвариантной величиной, может служить мерцающая тень объекта в комнате, освещаемой пламенем из камина. Очевидно, что тень меняется в зависимости от того, как горит огонь и где находится камин, но у нас нет никаких сомнений, что за тень отвечает реальный, неизменный объект. Используя пространство-время, мы хотим вывести физику из тени и отследить соотношения между реальными объектами.

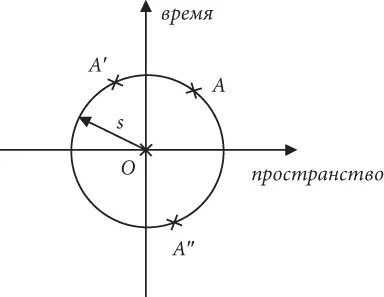
Рис. 5

Тот факт, что два разных наблюдателя могут измерить разные значения x и t , получив при этом одинаковое значение s , имеет очень важное следствие, которое довольно просто визуализировать. На рис. 5 показана окружность с центром в точке O (событие, соответствующее пробуждению в семь утра), с радиусом s . Поскольку пока мы используем формулу Пифагора для расчета расстояния, каждая точка окружности одинаково удалена от O . Это вполне очевидно: расстояние представляет собой радиус окружности. Точки вне круга находятся дальше от O , а точки внутри круга – ближе к O . Но наша гипотеза гласит, что s – это расстояние в пространстве-времени между событиями O и A . Другими словами, событие A может находиться где угодно на окружности, и при этом его расстояние в пространстве-времени от события O будет равно s . В какой же точке окружности должно располагаться событие A ? Это зависит от того, кто измеряет x и t . Мне, находящемуся в доме, точно известно, что x = 10 метров и t = 1 час. На диаграмме эта точка отмечена как A . Для наблюдателя в летящей с огромной скоростью ракете расстояние в пространстве x и расстояние во времени t изменятся, но если s при этом останется неизменным, событие должно по-прежнему находиться где-то на окружности. Так что разные наблюдатели будут указывать разные положения в пространстве и времени для одного и того же события, но при этом станут подчиняться одному ограничению – все они будут находиться на указанной окружности. Обозначим два возможных положения события как A ′ и A ″. Что касается положения A ′, то оно малоинтересно, а вот положение A ″ заслуживает внимания. Здесь действительно происходит нечто весьма любопытное. A ″ имеет отрицательное расстояние во времени относительно O . Другими словами, A ″ происходит до O . Оно теперь находится в прошлом относительно O . Это мир, в котором вы завершаете завтрак до того, как просыпаетесь! Такое обстоятельство – очевидное нарушение принятой нами аксиомы о выполнении принципа причинности.