Согласно (11.10), меньшие k отвечают более низким энергетическим состояниям Е»Е 0 - 2 А. Когда k по величине растет (все равно, в положительную или отрицательную сторону), то энергия сперва растет, а потом при k =± p // b достигает максимума, как показано на фиг. 11.3. Для k, больших, чем p / /b, энергия опять начала бы убывать. Но такие k рассматривать не стоит, они не приведут к каким-либо новым состояниям, а просто повторяют те состояния, которые уже появлялись при меньших k. Вот как в этом можно убедиться. Рассмотрим состояние наинизшей энергии, для которого k= 0. Тогда при всех х n коэффициент а (х n ) будет один и тот же [см. (11.10)1. Та же самая энергия получилась бы и при k = 2 p / /b. Тогда из
(11.10) следовало бы
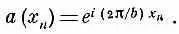
Но, считая, что начало координат приходится на х 0 , можно положить х n = nb, и тогда а (х n ) превратится в
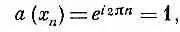
т. е. состояние, описываемое этими а (х n ), физически ничем не будет отличаться от состояний при k= 0. Оно не представляет особого решения.
В качестве другого примера возьмем k=p /4 b . Вещественная часть а (х n ) изображена на фиг. 11.4 кривой 1.
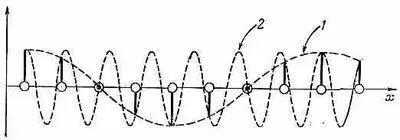
Фиг. 11.4. Пара значений к, представляющих одну и ту же физическую ситуацию. Кривая 1—для k=p/4b, кривая 2 —для k=7p/4b.
Если бы k было в семь раз больше (k=7p / /4b), то вещественная часть а (х n ) менялась бы так, как показано на кривой 2. (Сама косинусоида смысла не имеет, важны только ее значения в точках х n .
Кривые нужны просто для того, чтобы было видно, как все меняется.) Вы видите, что оба значения k во всех х n дают одинаковые амплитуды.
Вывод из всего этого состоит в том, что все возможные решения нашей задачи получатся, если взять k только из некоторой ограниченной области. Мы выберем область от -p /b до +p/ b (она показана на фиг. 11.3). В этой области энергия стационарных состояний с ростом абсолютной величины k возрастает.
Еще одно побочное замечание о том, с чем было бы забавно повозиться. Представьте, что электрон может не только перепрыгивать к ближайшим соседям с амплитудой iA/h, но имеет еще возможность одним махом перепрыгивать и к следующим за ними соседям с некоторой другой амплитудой iB/h. Вы опять обнаружите, что решение можно искать в форме а п = e ikx , этот тип решений является универсальным. Вы также увидите, что стационарные состояния с волновым числом k имеют энергию E 0-2 A cos kb- 2 B cos2 kb. Это означает, что форма кривой Е как функции k не универсальна, а зависит от тех частных допущений, при которых решается задача. Это не обязательно косинусоида, и она даже не обязательно симметрична относительно горизонтальной оси. Но зато всегда верно, что кривая вне интервала (-p/ b , p/ b ) повторяется, так что заботиться о других значениях k не нужно.
Посмотрим еще внимательнее на то, что происходит при малых k, когда вариации амплитуд между одним х n и соседним очень маленькие. Будем отсчитывать энергию от такого уровня, чтобы было Е 0 = 2 А; тогда минимум кривой фиг. 11.3 придется на нуль энергии. Для достаточно малых k можно написать
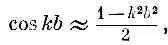
и энергия (11.13) превратится в

Получается, что энергия состояния пропорциональна квадрату волнового числа, описывающего пространственные вариации
амплитуд С n .
§ 3. Состояния, зависящие от времени
В этом параграфе мы хотим подробнее обсудить поведение состояний в одномерной решетке. Если для электрона амплитуда того, что он окажется в х n , равна С n , то вероятность найти его там будет | С n | 2. Для стационарных состояний, описанных уравнением (11.12), эта вероятность при всех х n одна и та же и со временем не меняется. Как же отобразить такое положение вещей, которое грубо можно было бы описать, сказав, что электрон определенной энергии сосредоточен в определенной области, так что более вероятно найти его в каком-то одном месте, чем в другом? Этого можно добиться суперпозицией нескольких решений, похожих на (11.12), но со слегка различными значениями k и, следовательно, с различными энергиями. Тогда, по крайней мере при t =0, амплитуда С n вследствие интерференции различных слагаемых будет зависеть от местоположения, в точности так же, как получаются биения, когда имеется смесь волн разной длины [см. гл. 48 (вып. 4)]. Значит, можно составить такой «волновой пакет», что в нем будет преобладать волновое число k 0, но будут присутствовать и другие волновые числа, близкие к k 0 .
Читать дальше

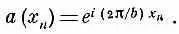
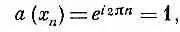

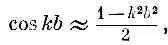




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


