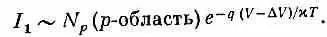
Этот ток превосходит ток I 0в 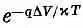 раз. Значит, между I 1и I 0существует следующая связь:
раз. Значит, между I 1и I 0существует следующая связь:

Ток из p -области при приложении внешнего напряжения D V растет по экспоненте. А ток положительных носителей из n- области остается постоянным, пока D V не слишком велико.
Достигая барьера, эти носители по-прежнему будут видеть перед собой идущий под гору потенциал и будут все скатываться в p -область. (Если D V больше естественной разности потенциалов V, положение может измениться, но что случается при таких высоких напряжениях, мы рассматривать не будем.) В итоге ток положительных носителей I , текущий через переход, будет определяться разницей токов в обе стороны:
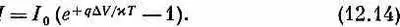
Дырочный ток I течет в n -область. Там дырки диффундируют в самую глубь n -области и могут, вообще говоря, аннигилировать на основной массе отрицательных носителей электронов. Убыль электронов, теряемых при этой аннигиляции, восполняется током электронов из внешнего контакта материала n -типа.
Когда D V =0, то и ток в (12.14) равен нулю. Если D V положительна, ток с напряжением резко растет, а если D V отрицательна, знак тока меняется, но экспоненциальный член вскоре становится пренебрежимо малым, и отрицательный ток никогда не превышает I 0— величины, которая, по нашему предположению, очень мала. Этот обратный ток I 0ограничен той слабой плотностью, которой обладают неосновные носители в n -области перехода.
Если вы проведете в точности тот же анализ для тока отрицательных носителей, текущего через переход, сперва без внешней разности потенциалов, а после с небольшой приложенной извне разностью потенциалов D V , то для суммарного электронного тока вы опять получите уравнение, похожее на (12.14). Поскольку полный ток есть сумма токов носителей обоего рода, то (12.14) применимо и к полному току, если только отождествить I 0с максимальным током, который может течь при перемене знака напряжения.
Вольтамперная характеристика (12.14) показана на фиг. 12.10.
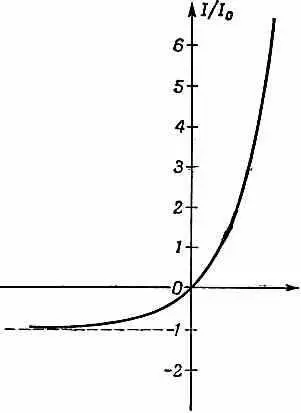
Фиг. 12.10. Зависимость тока через переход от приложенного к нему напряжения.
Она демонстрирует нам типичное поведение кристаллических диодов, подобных тем, которые применяются в современных вычислительных машинах. Нужно только заметить, что (12.14) справедливо лишь при невысоких напряжениях. При напряжениях, сравнимых с естественной внутренней разностью потенциалов V (или превышающих ее), в игру входят новые явления и ток уже не подчиняется столь простому уравнению.
Быть может, вы вспомните, что в точности такое же уравнение мы получили, говоря о «механическом выпрямителе» — храповике и собачке [см. гл. 46 (вып. 4)]. Мы получали те же уравнения, потому что лежащие в их основе физические процессы весьма схожи.
§ 6. Транзистор
Пожалуй, самым важным применением полупроводников является изобретение транзистора. Состоит он из двух полупроводниковых переходов, расположенных вплотную друг к другу, и работа его частично опирается на те же принципы, которые мы только что описывали, говоря о полупроводниковом диоде — выпрямляющем переходе. Предположим, что мы изготовили из германия небольшой брусочек, составленный из трех участков: p -область, n- область и опять p -область (фиг. 12.11,а). Такое сочетание именуется p—n—p -транзистором. Ведут себя эти переходы в транзисторе примерно так же, как описывалось в предыдущем параграфе. В частности, в каждом переходе должен наблюдаться перепад потенциала — падение потенциала из n -области в каждую из p -областей. Если внутренние свойства обеих p -областей одинаковы, то потенциал вдоль брусочка меняется так, как показано на фиг. 12.11, б .
Теперь представьте себе, что каждая из трех областей подключена к источнику внешнего напряжения (фиг. 12.12, а ). Будем относить все напряжения к контакту, присоединенному к левой p -области, так что на этом контакте потенциал будет равен нулю.
Читать дальше

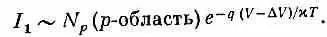
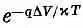 раз. Значит, между I 1и I 0существует следующая связь:
раз. Значит, между I 1и I 0существует следующая связь:




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


