
Знаки r и q одинаковы (отрицательны), и поскольку r — величина постоянная, то я могу положить r q / m =-(некоторая постоянная). Тогда
J=-(некоторая постоянная) А. (19.21)
Это уравнение впервые предложили братья Лондон, чтобы объяснить экспериментальные наблюдения над сверхпроводимостью, задолго до того, как люди уяснили себе квантовомеханическое происхождение эффекта.
Мы теперь можем подставить (19.20) в уравнения электромагнетизма и определить поля. Векторный потенциал связан с плотностью тока уравнением

Если вместо Jя подставлю (19.21), то получу

где l 2—просто новая постоянная

Теперь можно попробовать решить это уравнение относительно Аи детальнее посмотреть, что там происходит. Например, в одномерном случае у (19.23) имеются экспоненциальные решения вида е - l x и е + l х . Эти решения означают, что векторный потенциал обязан экспоненциально убывать по мере удаления от поверхности внутрь образца. (Возрастать он не может — будет взрыв.) Если кусок металла очень велик по сравнению с 1/l, то поле проникнет внутрь только в тонкий слой у поверхности толщиной около 1/l. Все остальное место внутри проводника будет свободно от поля, как показано на фиг. 19.3.
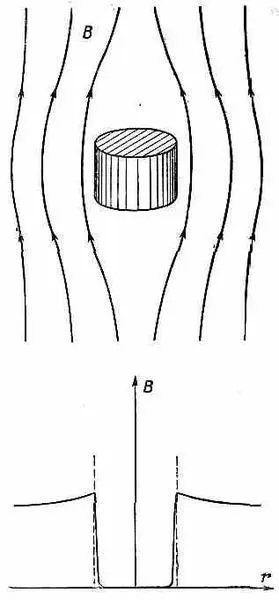
Фиг. 19.3. Сверхпроводящий цилиндр в магнитном поле (а) и магнитное поле В как функция от r (б).
Этим и объясняется явление Мейсснера.
Какова же эта «глубина проникновения» 1/l? Вы помните, что r 0— «электромагнитный радиус» электрона (2,8·10 -1 3 см )—выражается формулой
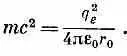
Вы помните также, что q вдвое больше заряда электрона, так что
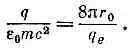
Записав r в виде q e N, где N — число электронов в кубическом сантиметре, мы получим

У такого металла, как свинец, на каждый кубический сантиметр приходится 3·10 22атомов, и если каждый атом снабдит нас одним электроном проводимости, то 1/l будет порядка 2·10 -5 см . Это дает вам порядок величины эффекта.
§ 7. Квантование потока
Уравнение Лондонов (19.21) было предложено, чтобы объяснить наблюдавшиеся при сверхпроводимости явления, включая эффект Мейсснера. Однако в последнее время прозвучали и более поразительные предсказания. Одно из предсказаний Лондонов было таким своеобразным, что никто даже не обратил на него особого внимания. Об этом я и расскажу. На сей раз возьмем сверхпроводящее кольцо, толщина которого по сравнению с 1/l велика, и посмотрим, что случится, если мы сперва наложим на кольцо магнитное поле, затем охладим кольцо до сверхпроводящего состояния, а потом уберем первоначальный источник поля В. Последовательность этих событий изображена на фиг. 19.4.
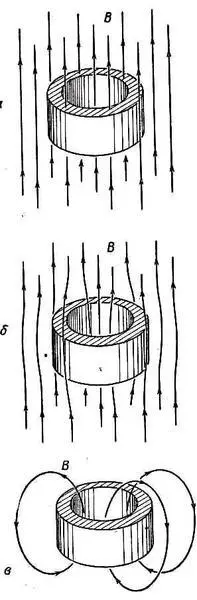
Фиг. 19,4. Кольцо в магнитном поле.
а — в нормальном, состоянии; б — в сверхпроводящем состоянии; в — после того, как внешнее поле убрали.
В нормальном состоянии (фиг. 19.4, а ) в теле кольца имеется магнитное поле. Когда кольцо становится сверхпроводящим, поле (как мы уже знаем) выталкивается из вещества кольца. Но тогда, как показано на фиг. 19.4, б , останется некоторый поток поля сквозь отверстие кольца. Если теперь убрать внешнее поле, то те линии поля, которые шли через отверстие, будут «заморожены» (фиг. 19.4, в ). Поток Ф через центр сойти на нет не может, потому что дФ/дt должно быть все время равно контурному интегралу от Евдоль кольца, а Евнутри сверхпроводника равно нулю. И вот, когда мы убираем внешнее поле, то по кольцу начинает течь сверхпроводящий ток, цель которого — сохранить поток через кольцо неизменным. (Это старая идея о вихревых токах, только с нулевым сопротивлением.) Но все эти токи будут течь только у самой поверхности (на глубине не более 1/l), что следует из такого же анализа, как и проделанный для сплошного куска. Эти токи в состоянии сделать так, чтобы магнитное поле не попадало внутрь кольца, но зато все время держалось вокруг него.
Читать дальше






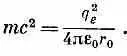
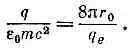





![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


