§ 3. Два рода импульсов
Уравнение для тока довольно интересно, хотя порой причиняет немало забот. Ток можно было бы считать чем-то вроде произведения плотности частиц на скорость. Плотность выглядела бы как yy*, так что здесь все в порядке. Каждый член в (19.12) напоминает типичное выражение для среднего значения оператора

Поэтому, быть может, следовало бы рассматривать его как скорость потока? Но тогда получается, что скорость с импульсом можно связать двояким образом, ведь с равным правом можно было бы считать, что скоростью должно быть отношение импульса к массе 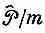 . Эти две возможности разнятся на вектор-потенциал.
. Эти две возможности разнятся на вектор-потенциал.
Оказывается, те же две возможности имелись еще в классической физике, и в ней тоже было найдено, что импульс можно определить двумя путями. Один можно назвать «кинематическим импульсом», но для абсолютной ясности я в этой лекции буду его называть « mv -импульсом». Это импульс, получаемый от перемножения массы на скорость. Другой, более математичный, более отвлеченный импульс, именуемый иногда «динамическим импульсом», а я его буду называть « р -импульс». Итак, у нас есть две возможности:
mv-импульс=m v , (19.14)
р-импульс=т v+ А . (19,15)
И вот оказывается, что в квантовой механике, включающей магнитные поля, с оператором градиента 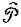 связан именно р -импульс, так что оператор скорости это (19.13).
связан именно р -импульс, так что оператор скорости это (19.13).
Здесь я хотел бы немного отклониться от темы и пояснить, почему так получается—отчего в квантовой механике должно быть нечто похожее на (19.15). Волновая функция меняется со временем, следуя уравнению Шредингера (19.3). Если бы я внезапно изменил векторный потенциал, то в первое мгновение волновая функция не изменилась бы, а изменилась бы только скорость ее изменения. Теперь представьте себе, что случится в следующих обстоятельствах. Пусть имеется длинный соленоид, в котором я создаю поток магнитного поля (поля В), как показано на фиг. 19.2.
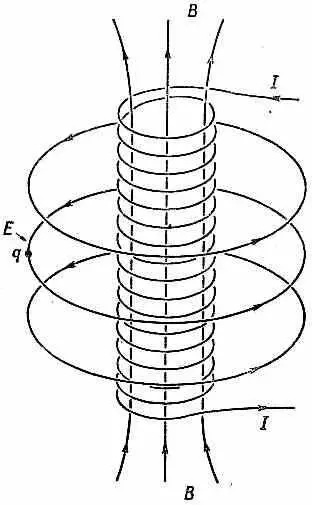
Фиг. 19.2. Электрическое поле снаружи соленоида, ток в котором увеличивается.
А поблизости сидит заряженная частица. Допустим, что этот поток почти мгновенно с нуля вырастает до какого-то значения. Сперва векторный потенциал равен нулю, а потом я его включаю. Это означает, что я внезапно создаю круговой вектор-потенциал А. Вы помните, что криволинейный интеграл от А вдоль петли это то же самое, что поток поля В сквозь петлю [см. гл. 14, § 1 (вып. 5)]. И что же происходит, когда я мгновенно включаю векторный потенциал? Согласно квантовомеханическому уравнению, внезапное изменение А не вызывает внезапного изменения y; волновая функция пока та же самая. Значит, и градиент не изменился.
Но вспомните, что происходит электрически, когда я внезапно включаю поток. В течение краткого времени, пока поток растет, возникает электрическое поле, контурный интеграл от которого равен скорости изменения потока во времени
Е=- д A /дt. (19.16)
Если поток резко меняется, то электрическое поле достигает огромной величины и оказывает сильное воздействие на частицу. Эта сила равна произведению заряда на электрическое поле; стало быть, в момент появления потока частица получает полный импульс (т. е. изменение в m v ), равный - q А. Иными словами, если вы подействуете на заряд векторным потенциалом, включив его внезапно, то этот заряд немедленно схватит mv-импульс, равный - q А. Но имеется нечто, не меняющееся немедленно,— это разность между m vи - q А.Стало быть, сумма p =m v+ q Aи есть то, что не меняется, если вы подвергаете вектор-потенциал внезапному изменению. Именно эту величину мы именуем p -импульсом, именно она играет важную роль в классической динамике; она же оказывается существенной и в квантовой механике. Эта величина зависит от характера волновой функции и является преемником оператора
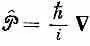
Читать дальше


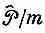 . Эти две возможности разнятся на вектор-потенциал.
. Эти две возможности разнятся на вектор-потенциал.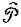 связан именно р -импульс, так что оператор скорости это (19.13).
связан именно р -импульс, так что оператор скорости это (19.13).



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


