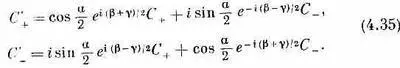
Итак, начав просто с некоторых предположений о свойствах пространства, мы вывели преобразование амплитуды при любом повороте. Это означает, что если нам известны амплитуды того, что любое состояние частицы со спином 1/ 2перейдет в один из двух пучков прибора Штерна — Герлаха S с осями х, у, z, то мы можем подсчитать, какая часть перейдет в каждый пучок в приборе Т с осями х', у' и z'. Иначе говоря, если имеется состояние y частицы со спином 1/ 2, у которого амплитуды пребывания вверху и внизу по отношению к оси z системы координат х, у, z равны С +=<+|y> и С -=<-|y>, то тем самым мы знаем амплитуды С + и C -пребывания вверху и внизу по отношению к оси z' любой другой системы х', у", z' , Четверка коэффициентов в (4.35) — это члены «матрицы преобразования», с помощью которой можно проецировать амплитуды частицы со спином 1/ 2в другие системы координат.
Теперь решим несколько примеров, чтобы посмотреть, как все это работает. Возьмем следующий простой вопрос. Пустим атом со спином 1/ 2через прибор Штерна — Герлаха, пропускающий только состояние (+z). Какова амплитуда того, что атом окажется в состоянии (+ x )? Ось + х — это все равно, что ось +z' системы, повернутой на 90° вокруг оси у. Поэтому в этой задаче проще воспользоваться выражением (4.32), хотя, конечно, можно применить и полное уравнение (4.35). Поскольку С + =1 и С - =0, то получится С' + =1/Ц2. Вероятности -это квадраты модулей этих амплитуд; таким образом, 50% шансов за то, что частица пройдет сквозь прибор, отбирающий состояние ( +х ) . Если бы мы поинтересовались состоянием (- х ) , то амплитуда оказалась бы -1/Ц2, что опять дало бы вероятность 1/ 2, чего и следовало ожидать из симметрии пространства. Итак, если частица находится в состоянии (+z), то ей в равной степени вероятно побывать в состояниях (+ x ) и (- х ) . Но фазы противоположны.
Ось у тоже без претензий. Частица в состоянии (+ z ) имеет равные шансы быть в состоянии (+у) или (- у ) . Но теперь (согласно формуле для поворота на -90° вокруг оси х) амплитуды суть l/Ц2 и - i /Ц2. В этом случае разница в фазах двух амплитуд уже не 180°, как было для ( +х )и (- х ) , а 90°. В этом-то и проявляется различие между х и у.
Вот еще пример. Пусть нам известно, что частица со спином 1/ 2находится в состоянии y, поляризованном вверх относительно оси А, определяемой углами q и j (фиг. 4.10).
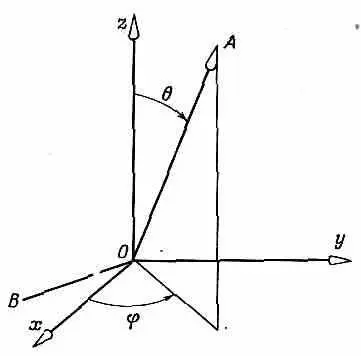
Фиг. 4.10. Ось А, определяемая полярными углами q и j .
Мы хотим знать амплитуду +|y> того, что частица относительно оси z окажется в состоянии «вверх», и амплитуду -|y> того, что она окажется в состоянии «вниз» относительно той же оси z. Эти амплитуды мы можем найти, вообразив, что А есть ось z' системы, у которой ось х' направлена произвольно, скажем лежит в плоскости, образованной А и z. Тогда можно перевести систему А в систему х, у, z тремя поворотами. Во-первых, надо сделать поворот на -p/2 вокруг оси A , что переведет ось x в линию В на рисунке. Затем повернуть на — 0 вокруг линии В (вокруг новой оси х системы А), чтобы ось А попала на ось z. И, наконец, повернуть вокруг оси z на угол (p/2-j).

Вспоминая, что вначале было только одно состояние (+) по отношению к А, получаем
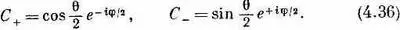
Мы хотели бы напоследок подытожить результаты этой главы в форме, которая окажется полезной для нашей дальнейшей работы. Во-первых, напомним, что наш основной результат (4.35) может быть записан в других обозначениях. Заметьте, что (4.35)— это то же самое, что и (4.4) Иначе говоря, в (4.35) коэффициенты при С +=<+S|y> и C' -= <- S |y> суть как раз амплитуды < jT | iS >в (4.4), амплитуды того, что частица в состоянии i по отношению к S окажется в состоянии j по отношению к Т (когда ориентация Т по отношению к S дается углами a, b и g) . Мы их также называли R TS ji в выражении (4.6). (Чего-чего, а обозначений у нас хватало!) Например,  — это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.
— это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.
Читать дальше

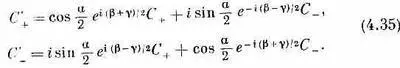


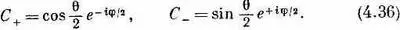
 — это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.
— это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.


![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


