Поскольку это скаляр, то он должен оставаться одним и тем же для любой ориентации спина. Предположим, что мы случайно выбрали образец какой-либо атомной системы и произвели измерения либо величины J 2 x , либо J 2 y, либо J 2 z — среднее
значение любой из них должно быть тем же самым. (Ни одно из направлений не имеет особого преимущества перед любым другим.) Следовательно, среднее значение J· Jравно просто утроенной средней величине любой компоненты, скажем J 2 z :
· J> cp =3 2 z >.
Но поскольку J· Jпри любой ориентации одно и то же, его среднее, разумеется, будет постоянной величиной
J· J= 32 z> cp. (34.24)
Если же мы теперь скажем, что то же самое уравнение будет использоваться и в квантовой механике, то можем легко найти 2 z> ср. Нам просто нужно взять сумму (2j+1) возможных значений J 2 zи поделить ее на число всех значений:
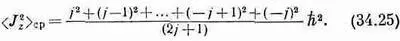
Вот что получается для системы со спином 3/ 2:
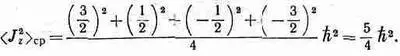
Отсюда мы заключаем, что
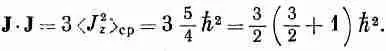
На вашу долю остается доказать, что соотношение (34.25) вместе с (34.24) дает в результате

Хотя в рамках классической физики мы бы думали, что наибольшее возможное значение z-компоненты Jравно просто абсолютной величине J, именно Ц( J· J), в квантовой механике максимальное значение J z всегда немного меньше его, ибо jh всегда меньше Ц[j(j+1)]h. Момент количества движения никогда не направлен «полностью вдоль оси z».
§ 8. Магнитная энергия атомов
Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения соотношением (34.6):

где - q e — заряд, а m — масса электрона.
Атомные магнитики, будучи помещены во внешнее магнитное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в направлении поля. Мы знаем, что
U маг =-m·В.(34.28) Выбирая ось z вдоль направления поля В, получаем
U маг =m z В. (34.29) А используя уравнение (34.27), находим
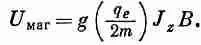
Согласно квантовой механике, величина J z может принимать только такие значения: jh, (j-1)h,...,- jh. Поэтому магнитная энергия атомной системы не произвольна, допустимы только некоторые ее значения. Например, максимальная величина энергии равна
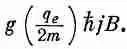
Величину q e h/2m обычно называют «магнетоном Бора» и обозначают через m B :
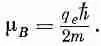
Возможные значения магнитной энергии будут следующими:
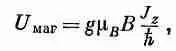
где J z /h принимает одно из следующих значений: j, (j-1), (j-2), ..., (-j+1), -j.
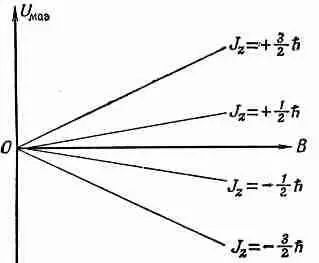
Другими словами, энергия атомной системы, помещенной в магнитное поле, изменяется на величину, пропорциональную полю и компоненте J г . Мы говорим, что энергия атомной магнитной системы «расщепляется магнитным полем на 2j+1 уровня». Например, атомы со спином j= 3 / 2 , энергия которых вне магнитного поля равна U 0, в магнитном поле будут иметь четыре возможных значения энергии. Эти энергии можно изобразить на диаграмме энергетических уровней наподобие фиг. 34.5.
Читать дальше

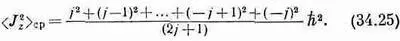
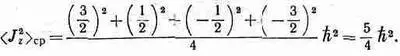
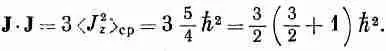


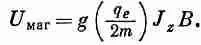
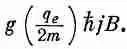
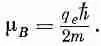
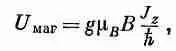




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
