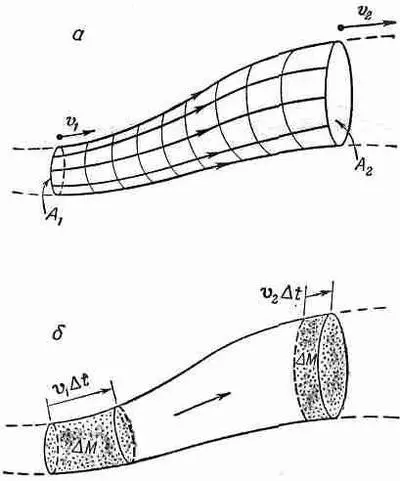
Фиг. 40.6. Движение жидкости в трубке.
Поскольку стенки трубки образуются линиями тока, то жидкость через них не протекает. Обозначим площадь на одном конце трубки через A 1, скорость жидкости через v 1 , плотность через r 1а потенциальную энергию через j 1. Соответствующие величины на другом конце трубки мы обозначим через A 2 , v 2 , r 2и j 2. После короткого интервала времени Dt жидкость на одном конце передвинется на расстояние v 1 D t, а жидкость на другом конце — на расстояние v 2Dt (см. фиг. 40.6, б). Сохранение массы требует, чтобы масса, которая вошла через A 1 была равна массе, которая
вышла через А 2 . Изменение масс в этих двух концах должно быть одинаково:
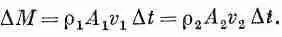
Таким образом, мы получаем равенство

Оно говорит нам, что при постоянном r скорость изменяется обратно пропорционально площади трубки тока.
Вычислим теперь работу, произведенную давлением в жидкости. Работа, произведенная над жидкостью, входящей со стороны сечения А 1 , равна р 1A 1v 1АDt, а работа, произведенная в сечении А 2 , равна p 2 A 2 v 2 D t. Следовательно, полная работа, произведенная над жидкостью, заключенной между A 1и А 2 , будет
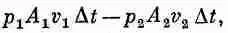
что должно быть равно возрастанию энергии массы жидкости DM при прохождении от А 1 до А 2 . Другими словами,
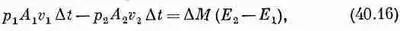
где Е 1 — энергия единицы массы жидкости в сечении А 1 , а Е 2 — энергия единицы массы в сечении А 2 . Энергию единицы массы жидкости можно записать в виде
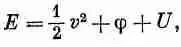
где 1/ 2 v 2 — кинетическая энергия единицы массы, j — потенциальная энергия, a U — дополнительный член, представляющий внутреннюю энергию единицы массы жидкости. Внутренняя энергия может соответствовать, например, тепловой энергии сжимаемой жидкости или химической энергии. Все эти величины могут изменяться от точки к точке. Воспользовавшись выражением для энергии в уравнении (40.16), получим
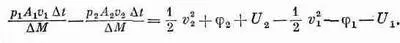
Но мы видели, что DМ=rDvDt, и получили
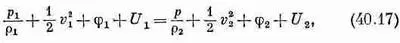
а это как раз приводит нас к результату Бернулли, где имеется дополнительный член, представляющий внутреннюю энергию. Если жидкость несжимаемая, то внутренняя энергия с обеих сторон одна и та же и мы снова убеждаемся в справедливости уравнения (40.14) вдоль любой линии тока.
Рассмотрим теперь некоторые простые примеры, в которых интеграл Бернулли позволяет нам сразу описать поток. Предположим, что из отверстия вблизи дна резервуара вытекает вода (фиг. 40.7).
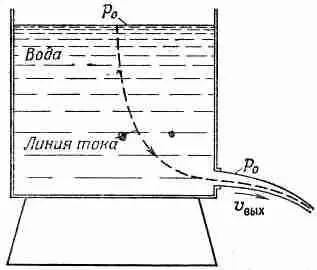
Фиг. 40.7. Вытекание жидкости из резервуара.
Рассмотрим случай, когда скорость потока v выхв отверстии гораздо больше скорости потока вблизи поверхности воды в резервуаре; другими словами, предположим, что диаметр резервуара настолько велик, что падением уровня жидкости можно пренебречь. (Мы могли бы при желании проделать и более аккуратные вычисления.) Давление на поверхность воды в резервуаре равно р 0 (атмосферному давлению), т. е. такое же, как и давление на бока струи. Напишем теперь уравнение Бернулли для линии тока наподобие той, что показана на фиг. 40.7. В верхней части резервуара скорость v мы примем равной нулю; гравитационный потенциал j здесь выберем тоже равным нулю. В отверстии же скорость равна v выха j =-gh , так что
Читать дальше


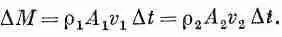

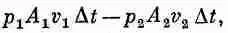
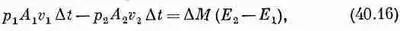
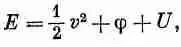
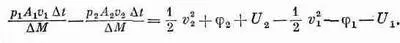
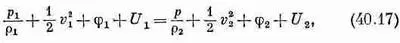




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
