Ясно, что для каждого поля В векторный потенциал А не единственный; существует много возможностей.
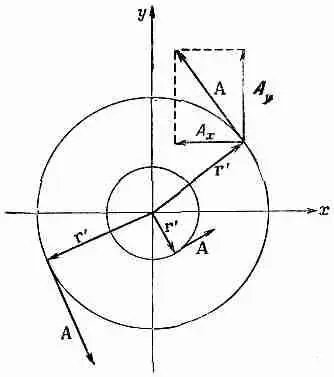
Фиг. 14.1. Однородное магнитное поле В, направленное по оси z, соответствует векторному потенциалу А (А=Вr'/2), который вращается вокруг оси z. т' — расстояние до оси z.
Третье решение [уравнение (14.8)] обладает рядом интересных свойств. Поскольку x-компонента пропорциональна -y, а y-компонента пропорциональна -+x, то вектор А должен быть перпендикулярен вектору, проведенному от оси z, который мы обозначим r' (штрих означает, что это не вектор расстояния от начала). Кроме того, величина А пропорциональна Ц(x 2+y 2) и, следовательно, пропорциональна r '. Поэтому А (для однородного поля) может быть записано просто
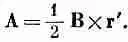
(14.9)
Векторный потенциал А равен по величине Br ' / 2 , и вращается вокруг оси z, как показано на фиг. 14.1. Если, например, поле В есть поле внутри соленоида вдоль его оси, то векторный потенциал циркулирует точно таким же образом, как и токи в соленоиде.
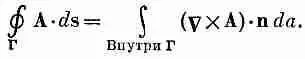
Векторный потенциал однородного поля может быть получен и другим способом. Циркуляция А вдоль любой замкнутой петли Г может быть выражена через поверхностный интеграл от СXА с помощью теоремы Стокса [уравнение (3.38), стр. 63]
(14.10)
Но интеграл справа равен потоку В сквозь петлю, поэтому
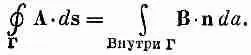
(14.11)
Итак, циркуляция А вдоль всякой петли равна потоку В сквозь петлю. Если мы возьмем круглую петлю радиуса r' в плоскости, перпендикулярной однородному полю В, то поток будет в точности равен
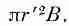
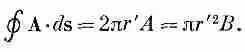
Если выбрать начало отсчета в центре петли, так что А можно считать направленным по касательной и функцией только от r', то циркуляция будет равна
Как и раньше, получаем
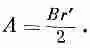
В только что разобранном примере мы вычисляем векторный потенциал из магнитного поля, обычно поступают наоборот. В сложных задачах всегда проще найти векторный потенциал, а затем уже из него найти магнитное поле. Сейчас мы покажем, как это можно сделать.
§ 2. Векторный потенциал заданных токов
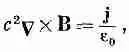
Раз В определяется токами, значит, и А тоже. Мы хотим теперь выразить А через токи. Начнем с нашего основного уравнения (14.2):
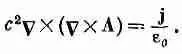
откуда, конечно, следует
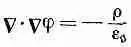
Это уравнение для магнитостатики; оно похоже на уравнение
(14.13)
для электростатики.
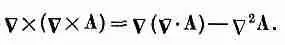
Наше уравнение (14.12) для векторного потенциала станет еще более похожим на уравнение для j, если переписать СX(СX А), используя векторное тождество [см. уравнение (2.58) стр. 44]
(14.14)
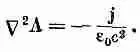
Поскольку мы выбрали С·А=0 (и теперь вы видите, почему), уравнение (14.12) приобретает вид
(14.15)
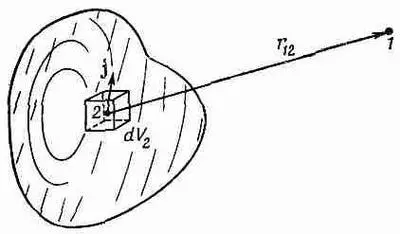
Фиг. 14.2. Векторный потенциал А в точке 1 определяется интегралом по элементам тока jdV во всех точках 2.
Это векторное уравнение, конечно, распадается на три уравнения
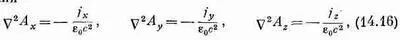
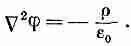
и каждое из этих уравнений математически идентично уравнению
(14.17)
Все, что мы узнали о нахождении потенциала для известного r, можно использовать для нахождения каждой компоненты А, когда известно j!
Читать дальше


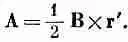
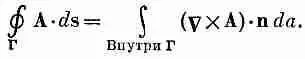
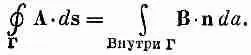
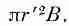
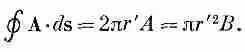
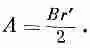
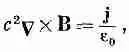
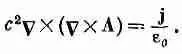
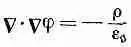
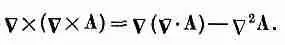
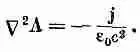

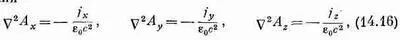
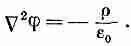




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

