Обсудим теперь влияние ориентации системы координат на физические законы. Давайте посмотрим, не будут ли нам снова полезны Мик и Джо. Чтобы избежать ненужных сложностей, предположим, что эти молодые люди находятся в одной точке пространства (мы уже показали, что их системы координат можно перемещать). Пусть оси системы координат Мика повернуты относительно системы координат Джо на угол q, Обе системы координат изображены на фиг. 11.2, где мы ограничились двумя измерениями.
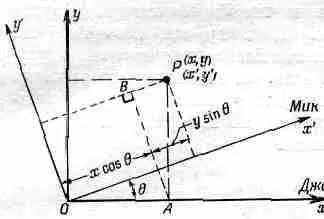
Фиг. 11.2. Две координатные системы, ориентированные по-разному.
Произвольная точка Р снабжается координатами (х, у) в системе Джо и (х', у') в системе Мика. Как и в предыдущем случае, начнем с того, что выразим координаты х' и у' через х, у и q. Для этого опустим из Р перпендикуляры на все четыре координатные оси и проведем АВ перпендикулярно PQ. Из чертежа ясно, что х' можно представить как сумму двух отрезков вдоль оси х', а у'— как разность двух отрезков вдоль АВ. Длины этих отрезков выражаются через х, у и 6; мы добавляем еще уравнение для третьей координаты:
х'=х cosq+ -у sinq,
y'=ycos q -x sinq, (11.5)
z'=z.
Теперь (мы поступали так и раньше) установим соотношения между силами, измеряемыми двумя наблюдателями. Предположим, что сила F, имеющая (с точки зрения Джо) составляющие F x и F y , действует на расположенную в точке Р на фиг. 11.2 частицу массы m . Для простоты сдвинем обе системы координат так, что начала их переместятся в точку Р, как показано на фиг. 11.3. Мик скажет нам, что сила, по его мнению, имеет составляющие F x ' и F y ' вдоль его осей.
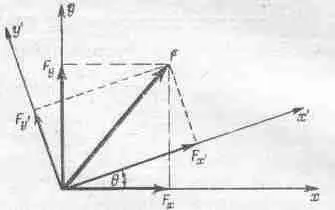
Фиг. 11.3, Составляющие сил в двух системах.
Составляющая F x , как и F y , имеет составляющие вдоль обеих осей х' и у'. Чтобы выразить F x ' через F x и F y , сложим составляющие этих сил вдоль оси х'; точно таким же образом можно выразить и F y ' через F х и F y . В результате получим
F x .=F x cosq+F y smq,
F y .=F y cosq-F x smq, (11.6)
F z ' = F z

Интересно отметить случайность, которая в дальнейшем окажется очень важной: формулы (11.5) и (11.6) для координат Р и составляющих F соответственно тождественны по форме. Как и раньше, предположим, что законы Ньютона справедливы в системе координат Джо и выражаются уравнениями (11.1). Снова возникает вопрос: может ли Мик пользоваться законами Ньютона, будут ли их предписания выполняться в повернутой системе координат? Другими словами, если предположить, что уравнения (11.5) и (11.6) дают связь между измеряемыми величинами, то верно ли, что
Чтобы проверить эти уравнения, вычислим левые и правые части независимо, а затем сравним результаты. Чтобы вычислить левые части, умножим уравнения (11.5) на m и продифференцируем их дважды по времени, считая угол 9 постоянным. Это дает
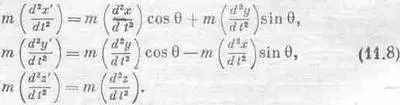
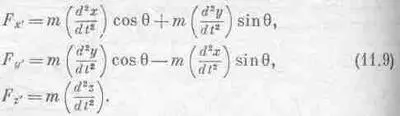
Вычислим правые части уравнений (11.7), подставив (11.1] в уравнения (11.6). Получаем
Глядите! Правые части уравнений (11.8) и (11.9) тождественны; значит, если законы Ньютона верны в одной системе координат, то ими можно пользоваться и в другой системе. Эти рассуждения заставляют нас сделать некоторые важные выводы: во-первых, никто не может утверждать, что избранная им система координат единственна, она может быть, конечно, более удобной при решении частных задач. Например, удобно, но не обязательно взять направление силы тяжести за одну из осей координат. Во-вторых, это означает, что любой механизм, если только он является самостоятельным устройством и обладает всем необходимым для создания силы, будет работать одинаково, как бы его ни повернули.
Читать дальше




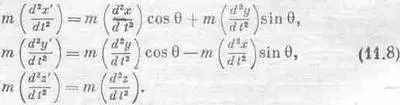
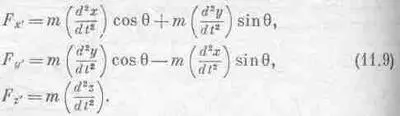



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


