* * *
На этом кончается наше путешествие. В таких случаях обычно принято писать заключение, делать выводы, подводить итоги. В книге о солитоне делать это, по-моему, рано. Солитон еще слишком молод и открыл нам лишь малую часть своих дарований. Да и может ли быть какой-нибудь конец у истории о бесконечно разнообразном детище бесконечной и изменчивой Природы... Продолжение?.. Да, продолжение истории обязательно будет! Только для этого понадобится работа молодого читателя этой книги, будущего создателя дерзких новых идей.
1. Получим решение уравнения (4.7) геометрически, придав показательной функции е -ω 0 t , которую записывают также в виде exp(ω 0 t ), геометрический смысл, аналогичный геометрическому смыслу тригонометрических функций.
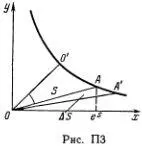
Построим на плоскости ( х, у ) график гиперболы у = 1/ х и обозначим буквой S площадь криволинейного треугольника ОО'А (рис. П1).
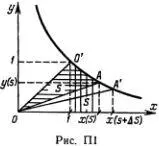
Тогда проекция точки А на ось Ох и есть x ( S ) = ехр( S ). Это определение можно пояснить по-другому. Площадь ОО'А равна площади О'Ах ( S )1, так как эти фигуры получаются вычитанием равновеликих треyгольников OAx ( S ) И OO' 1 из одной и той же фигуры OO'Ax ( S ). Площадь O'Ax ( S )1 по обычному определению есть натуральный логарифм: S = log ex ( S ) = ln x ( S ), а x ( S ) = exp( S ) — это просто обратная функция. Ясно теперь, что число е определяется условием е = x (1).
Если точка А движется по гиперболе так, что площадь S равномерно растет со временем, т. е. S = ω 0 t , то x ( S ) = exp(ω 0 t ), а y ( S ) = 1/ x ( S ) = exp(-ω 0 t ). С помощью этого построения легко найти производную показательной функции. Площадь Δ S бесконечно малого прямоугольника x ( S ) AA'x ( S + ΔS) равна [ x ( S + Δ S ) - x ( S )] y ( S ) = Δ S , откуда следует, что
[ x ( S + Δ S ) - x ( S )]1/Δ S = 1/ y (S) = x ( S ),
т. е. Δ( e S )/Δ S = е S . Когда S = ω 0 t , то отсюда следует, что
Δ( e S )/Δ t = Δ x /Δ t = ω 0 e ω 0 t ,
т. е. х' = ω 0 х . Точно так же у' = -ω 0 у , и мы показали, что у = ехр (-ω 0 t ) — решение уравнения (4.7). Самое общее решение можно получить, если взять S = ω 0( t + t 0), т. е. просто сдвинуть начало отсчета времени.
Аналогия с геометрическим определением тригонометрических функций cos(ω 0 t ) и sin(ω 0 t ) теперь должна быть ясной. Они определялись как проекции на координатные оси точки, движущейся по окружности единичного радиуса. Поэтому площадь сектора, «заметаемого» радиусом, также равномерно нарастала со временем: S = ω 0 t .
Еще ближе аналогия тригонометрических функций с гиперболическими функциями. Построим на таком же рисунке, как и рис. П1 взаимно перпендикулярные оси ОУ и ОХ (рис. П2).
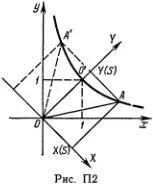
Поделенные на 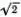 проекции X ( S ) и Y ( S ) точки А на эти оси называются гиперболическим синусом и гиперболическим косинусом аргумента S и обозначаются следующим образом:
проекции X ( S ) и Y ( S ) точки А на эти оси называются гиперболическим синусом и гиперболическим косинусом аргумента S и обозначаются следующим образом:
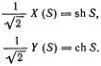
Эти функции похожи на sin S и cos S . Ясно, что их легко выразить через ехр ( S ) и ехр (- S ), но полезно знать и геометрическое определение, исходя из которого можно найти все основные свойства показательной и гиперболических функций.
Самое главное свойство показательной функции, которое можно было бы взять за определение, выражается очень просто: e S 1+ S 2= e S 1 • e S 2 . Доказывается оно геометрическим рассуждением, провести которое мы предлагаем читателю. Покажите также, что sh S = 1/2 ( e S - e -S ), ch S = 1/2 ( e S + e -S ).
2. Найдем теперь геометрическим построением решение уравнения (4.6). Обозначим 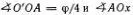 = ψ (рис. ПЗ).
= ψ (рис. ПЗ).
Отсюда очевидно, что ψ = (π - φ)/4 и tg ψ = exp(- S )/exp( S ) = exp(-2 S ). Приращение площади ΔS при малом смещении точки А по гиперболе можно записать как площадь малого сектора с радиусом ( ОА )  ( ОА' ) и углом -Δψ =
( ОА' ) и углом -Δψ = 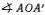 , т. е. Δ S = -½Δψ·( ОА ) 2. Так как ( ОА ) = ехр( S )/cos ψ, то отсюда следует, что
, т. е. Δ S = -½Δψ·( ОА ) 2. Так как ( ОА ) = ехр( S )/cos ψ, то отсюда следует, что
Читать дальше



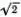 проекции X ( S ) и Y ( S ) точки А на эти оси называются гиперболическим синусом и гиперболическим косинусом аргумента S и обозначаются следующим образом:
проекции X ( S ) и Y ( S ) точки А на эти оси называются гиперболическим синусом и гиперболическим косинусом аргумента S и обозначаются следующим образом: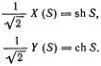
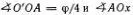 = ψ (рис. ПЗ).
= ψ (рис. ПЗ).
 ( ОА' ) и углом -Δψ =
( ОА' ) и углом -Δψ = 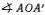 , т. е. Δ S = -½Δψ·( ОА ) 2. Так как ( ОА ) = ехр( S )/cos ψ, то отсюда следует, что
, т. е. Δ S = -½Δψ·( ОА ) 2. Так как ( ОА ) = ехр( S )/cos ψ, то отсюда следует, что










