Кроме того, в процессе работы теоретиков над струнами выяснилось еще одно обстоятельство, которое напрочь закрывало возможность их применения к реальному миру адронов. Дело в том, что адронная струна должна быть «релятивистской» (удовлетворять требованиям специальной теории относительности) и «квантовой» (описываться на языке квантовой механики). Оказалось, что эти требования невозможно совместить в нашем обычном четырехмерном пространстве-времени. Внутренне непротиворечивая теория возможна лишь в 26-мерном пространстве-времени! Правда, изобретательные молодые теоретики Джон Шварц, Андре Неве и Пьер Рамон придумали более хитрую струну, существующую в 10-мерном пространстве-времени. В отличие от обычной струны, которую называют бозонной (или струной Намбу—Гото), по струне Неве—Шварца—Рамона распределены некие элементарные «магнитики» (вспомните нашу простую резинку со скрепками), которые «съедают» 16 лишних измерений, но большего достичь не удалось. Развитие теории этой струны привело к очень интересному открытию симметрий между бозонами и фермионами (эта совершенно новая и необычная симметрия называется суперсимметрией; хотя экспериментаторам пока не удалось обнаружить ее следов в реальном мире, многие теоретики успешно применяют ее в чисто теоретических исследованиях), но адронную струну это не спасало. По этим причинам к середине 70-х годов интерес физиков к струнной модели адронов ослабел, и лишь немногие энтузиасты продолжали размышлять о струнах, этих новых для физики, загадочных объектах.
Эти размышления вскоре вывели теоретиков на совершенно иные взгляды на струны. Одним из следствий теории струны было предсказание безмассовых частиц со спином 2. Это состояние возникает для струны, замкнувшейся в колечко. Образование таких замкнутых струн в квантовой теории совершенно неизбежно, а среди адронов частиц с нулевой массой и спином 2, безусловно, нет. Что же делать с этим предсказанием? Предоставим слово Джону Шварцу.
«В 1974—1975 гг. я работал с Джоэлем Шерком в Калтехе *). Мы были поражены тем фактом, что струнные теории никак не поддавались нашим многочисленным попыткам сдвинуть массы к другим значениям. В частности, в секторе замкнутых струн ...неизбежно появлялось безмассовое состояние со спином 2. В какой-то момент нам пришло в голову (не помню, кто сказал это первый — Джоэль или я), что, возможно, это состояние есть просто гравитон. Это невинное замечание привело к глубоким последствиям: это означало, что мы обсуждаем не адроны; это означало, что естественный масштаб длины для струн равен 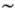 10 -33см (Планковская длина), а не 10 -13см... Самое главное следствие состояло в том, что возникала возможность построить квантовую теорию гравитации! Как только мы осознали, что мы имеем дело с гравитацией, наше отношение к лишним измерениям пространства резко изменилось. Мы поняли, что вполне разумно отнестись к ним серьезно как к реальным и физическим размерностям пространства (как того и требует теория), но истолковывать и в духе Калуцы—Клейна».
10 -33см (Планковская длина), а не 10 -13см... Самое главное следствие состояло в том, что возникала возможность построить квантовую теорию гравитации! Как только мы осознали, что мы имеем дело с гравитацией, наше отношение к лишним измерениям пространства резко изменилось. Мы поняли, что вполне разумно отнестись к ним серьезно как к реальным и физическим размерностям пространства (как того и требует теория), но истолковывать и в духе Калуцы—Клейна».
*) Знаменитый Калифорнийский Технологический Институт в г. Пасадина, США; в нем работал Ричард Фейнман, и продолжает работать Мюррей Гелл-Манн. — Примеч. авт.
Дадим необходимые пояснения. Уже давно было известно, что квантами гравитационного поля являются безмассовые частицы со спином 2. Известно было также, что на известных путях построить последовательную теорию квантовой гравитации никому не удалось и вряд ли удастся. Не видно было и путей к объединению гравитации с электрослабыми и сильными взаимодействиями, в которых переносчики взаимодействия, бозоны Янга—Миллса, имеют спин равный 1. Наконец, несколько слов об идеях Калуцы—Клейна.
В 1919 г. немецкий физик-теоретик Теодор Калуца (1885—1954), работавший в Кенигсбергском университете, сделал первую попытку объединения гравитационных и электромагнитных взаимодействий. Он применил идеи общей теории относительности к расширенному, пятимерному миру, включив электромагнитные потенциалы теории Максвелла в число гравитационных потенциалов пятимерного мира. Отличие электромагнитных потенциалов от гравитационных возникало благодаря предположению о независимости физических величин от пятой координаты (так что пятая координата — это в чистом виде улыбка Чеширского Кота). Это обстоятельство, конечно, делало теорию Калуцы довольно формальной и непривлекательной для физиков. Тем не менее она вызвала достаточно большой интерес.
Читать дальше

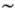 10 -33см (Планковская длина), а не 10 -13см... Самое главное следствие состояло в том, что возникала возможность построить квантовую теорию гравитации! Как только мы осознали, что мы имеем дело с гравитацией, наше отношение к лишним измерениям пространства резко изменилось. Мы поняли, что вполне разумно отнестись к ним серьезно как к реальным и физическим размерностям пространства (как того и требует теория), но истолковывать и в духе Калуцы—Клейна».
10 -33см (Планковская длина), а не 10 -13см... Самое главное следствие состояло в том, что возникала возможность построить квантовую теорию гравитации! Как только мы осознали, что мы имеем дело с гравитацией, наше отношение к лишним измерениям пространства резко изменилось. Мы поняли, что вполне разумно отнестись к ним серьезно как к реальным и физическим размерностям пространства (как того и требует теория), но истолковывать и в духе Калуцы—Клейна».










