Читатель, желающий подробнее ознакомиться с этими замечательными явлениями, может обратиться к книге В. С. Эдельмана «Вблизи абсолютного нуля» (М.: Наука, 1983. Библиотечка «Квант», вып. 26). Здесь мы скажем только несколько слов о вихрях, многие интересные свойства которых были открыты американским физиком Р. Фейнманом. Вихри в сверхтекучем гелии устроены примерно так же, как в идеальной жидкости Эйлера. Самое важное отличие состоит в том, что «сила» отдельного вихря квантована! Точный смысл этого утверждения состоит в следующем. Если в сверхтекучем гелии есть прямолинейная вихревая нить OO' (рис. 7.15), т. е. вихревое движение сосредоточено внутри очень тонкой трубки, то вне этой трубки на расстоянии r от нити скорость жидкости равна v = 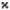 /2π r *). Здесь
/2π r *). Здесь 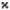 = nh / m He, а n — целое число ( h — постоянная Планка, m Не— масса атома гелия). В обычной жидкости скорость вокруг вихревой нити распределена по такому же закону, но сила вихря
= nh / m He, а n — целое число ( h — постоянная Планка, m Не— масса атома гелия). В обычной жидкости скорость вокруг вихревой нити распределена по такому же закону, но сила вихря 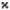 может быть любой. Квантование силы вихря — одно из проявлений квантовых свойств сверхтекучих жидкостей.
может быть любой. Квантование силы вихря — одно из проявлений квантовых свойств сверхтекучих жидкостей.
*) Там, где скорость распределена по такому закону, движение не вихревое. Это можно доказать точно так жe, как мы доказали, что при v = ω r движение вихревое.
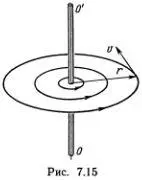
Подобные вихри могут возникать и в некоторых сверхпроводниках. Так как «электронная жидкость» переносит заряд, то при ее движении возникает электрический ток, а следовательно, и магнитное поле. С вихрем в сверхпроводнике поэтому должно быть связано магнитное поле, сосредоточенное в трубке, окружающей нить OO' на рис. 7.15. Хорошо известно, однако, что магнитное поле не может проникнуть в толщу сверхпроводника, так как в идеальной жидкости сверхпроводящих электронов магнитное поле мгновенно наводит токи, которые полностью его компенсируют. Если же увеличивать магнитное поле, то при достаточно большом его значении сверхпроводимость просто разрушится. Так ведут себя классические сверхпроводники (олово, алюминий, свинец и др.), которые называют сверхпроводниками первого рода.
Существуют, однако, сверхпроводники второго рода (например ниобий), которые реагируют на приложенное к ним магнитное поле иначе. Достаточно сильное магнитное поле может проникнуть в сверхпроводник второго рода, но только в виде вихревых нитей. Магнитное поле как бы «просверливает» себе отверстия в толще сверхпроводящей жидкости. Вблизи вихря, где магнитное поле максимально, остается только нормальная электронная жидкость, а в сверхпроводящей жидкости циркулируют незатухающие токи, не выпускающие поле за пределы трубки. Из-за того что электронная жидкость заряжена, вихрь в сверхпроводнике несколько отличается от вихря в жидком гелии — скорости сверхпроводящих электронов убывают при увеличении r быстрее, чем скорости сверхтекучих атомов гелия. Подобно вихрю в гелии, вихрь в сверхпроводнике квантован: произведение среднего значения магнитного поля в трубке ( Η ) на площадь трубки (Δ S ) равно n • hc /2 e , где n — целое число, с — скорость света, е — заряд электрона. Величину Ф 0= hc /2 e называют квантом магнитного потока .
Необычное поведение магнитного поля в сверхпроводниках второго рода было открыто Львом Васильевичем Шубниковым (1901—1945) еще в 1937 г. Однако причины этого поведения долгое время оставались непонятными, пока в 1950 г. В. Л. Гинзбург и Л. Д. Ландау не построили общую теорию сверхпроводников второго рода. Два года спустя А. А. Абрикосов ввел на ее основе представление о вихрях, которое показалось сначала чересчур смелым. Почти десятилетие понадобилось физикам для того, чтобы осознать, какой замечательный новый объект вошел в их науку, а многие возможности, заложенные в абрикосовских вихрях и их многочисленных «родственниках», не раскрыты и до сих пор.
Внешне вихри не очень похожи на классические, настоящие солитоны. Тем не менее между ними существует глубокая родственная связь. Наиболее ярко эта связь проявляется для вихрей в так называемом джозефсоновском переходе . Вихри в джозефсоновском переходе столь интересны, что с ними стоит познакомиться поближе. Они являются самыми настоящими солитонами и при ближайшем рассмотрении оказываются очень похожими на дислокации.
Читать дальше

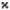 /2π r *). Здесь
/2π r *). Здесь 











