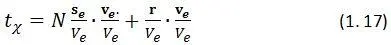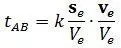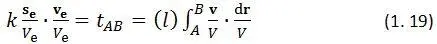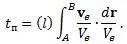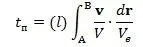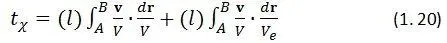Здесь и далее под выражением 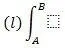 следует понимать единый символ криволинейного интеграла по кривой ( l ), а не произведение ( l ) на интеграл.
следует понимать единый символ криволинейного интеграла по кривой ( l ), а не произведение ( l ) на интеграл.
При V = 0 выражения (1. 15) и (1. 16) становятся неопределенными. Физический смысл этого таков: в системе, где ничего не движется, понятие времени теряет смысл и не является необходимым для полного описания системы.
Как известно из векторной алгебры, скалярное произведение (у нас (1. 15) и (1. 16)) не зависит от замены координат. Поэтому у нас время t AB , дифференциал времени, а также одновременность событий являются инвариантами по отношению к преобразованию координат.
Назовем часами устройство перемножающее скалярно некоторый нормированный эталонный вектор скорости v e/ V eна нормированные векторы r/ V eи s e/ V e; где r– радиус вектор часов, а s e– некоторый эталонный вектор, встроенный в часы и всегда того же направления, что и вектор v e. Часы суммируют результаты умножения по правилу:
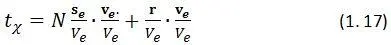
Здесь N – число периодов часов. Второе слагаемое в (1. 17) есть не что иное, как слагаемое переноса часов. Если часы при измерении времени находятся в покое в начале координат, то тогда:

Именно это время и является эталонным временем для сравнения с ним времени физического процесса. Измерить время t AB это значит узнать при каком k имеет место равенство:
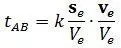
Это время равно интегралу (1. 16) то есть:
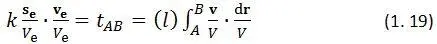
Если часы двигаются по кривой ( l ) от точки A до точки B независимо от других скоростей, то слагаемое переноса часов t пбудет равно интегралу:
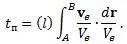
При этом скорость v eнаправляется по касательной к траектории движения часов в заранее выбранном положительном направлении. Другими словами: слагаемое переноса часов равно времени, которое затратит материальная точка, двигаясь по данной кривой вместо часов со скоростью равной v e. В другом случае при измерении времени часы могут двигаться вместе с материальной точкой, время движения которой они измеряют. Тогда на часах кроме времени (1. 19) появится еще слагаемое переноса часов, которое будет равно интегралу:
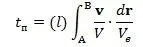
Здесь под знаком интеграла вместо множителя v e/ V eспециально поставлен единичный вектор v/ V , который подчеркивает, что согласно прежней договоренности, при таком движении мы направляем вектор v eпо направлению вектора v. Итак, показания часов будут равны сумме:
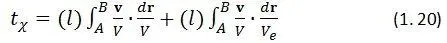
Здесь первое слагаемое – истинное время t , второе слагаемое – слагаемое переноса часов.
С точки зрения математика, введенное нами определение времени, допускает процессы, длительность которых равна нулю. Это такие процессы, в которых векторы d rи vперпендикулярны. Гипотеза о том, что и в природе существуют такие процессы, заслуживает отдельного изучения. Если эта гипотеза действительно имеет место, то нас уже не будет обескураживать тот факт, что сферический световой волновой фронт стягивается в материальную точку (квант) за время равное нулю. При таком преобразовании вектор скорости волнового фронта vперпендикулярен вектору d r. Точнее говоря: если волновой объект представляет собой шаровой слой, ограниченный двумя сферами (в пространстве) толщиной Δ s , то время его преобразования в точку (у нас в световой квант) будет равно: Δ t = Δ s / c , то есть будет равняться длительности волнового цуга (во времени).
1.Первый и второй постулаты теории относительности есть следствия попыток объяснить результаты физических измерений без учета того факта, что часы, будучи материальным объектом, обладают присущими таким объектам свойствами (слагаемым переноса).
Читать дальше


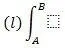 следует понимать единый символ криволинейного интеграла по кривой ( l ), а не произведение ( l ) на интеграл.
следует понимать единый символ криволинейного интеграла по кривой ( l ), а не произведение ( l ) на интеграл.