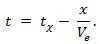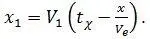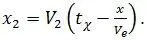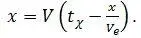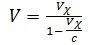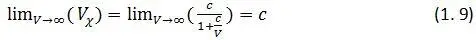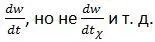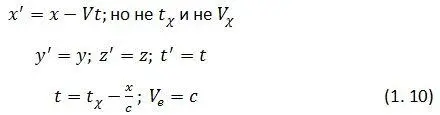Или

Таким образом, начиная с формул (1. 4) и (1. 5) нам следует отличать величины: 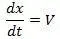 – истинная (или исправленная) скорость точки, а
– истинная (или исправленная) скорость точки, а 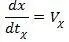 – скорость этой же точки определяемая по показаниям часов традиционным методом, без учета материальности часов. Из (1. 5) видно также, что модуль скорости V всегда больше модуля скорости V χ.
– скорость этой же точки определяемая по показаниям часов традиционным методом, без учета материальности часов. Из (1. 5) видно также, что модуль скорости V всегда больше модуля скорости V χ.
Пусть относительно системы координат O 1X 1 со скоростью V 1 движется другая система O 2X 2, а относительно системы O 2X 2 со скоростью V 2 движется материальная точка и вместе с ней с той же скоростью двигаются и часы. Какова скорость точки V относительно системы координат O 1X 1 ? В начальный момент времени t χ= t = 0 положим координаты точки, часов и второй системы координат O 2X 2 равными нулю, относительно первой системы O 1X 1.
Время, отсчитанное часами по достижению точкой координаты x (в первой системе координат), равно 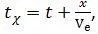 а истинное время движения равно:
а истинное время движения равно: 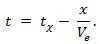
Путь, пройденный за это время системой O 2X 2 относительно системы O 1X 1 равен:
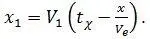
Путь, пройденный за это время точкой относительно системы O 2X 2 , равен:
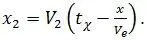
Путь, пройденный за это время точкой относительно системы O 1X 1 равен:
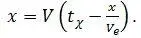
Этот путь равен сумме путей x 1 и x 2 , то есть:
x = x 1 + x 2 .
Из последних четырех равенств получаем:

Итак, для истинных времени и скоростей правило сложения скоростей классической механики остается в силе и никаких ограничений на величины скоростей при этом не накладывается.
С применением формулы (1. 6) нетрудно вывести аналогичную формулу и для векторов скоростей:

Как уже говорилось выше, для современной системы часов V e = c . Заменим в (1. 5) V e на c и получим:
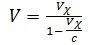
отсюда, выразив V χчерез V и c получим:

Пусть в выражении (1. 8) скорость V неограниченно возрастает. Тогда мы получим следующий предел:
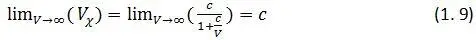
Выражение (1. 9) есть не что иное, как математическая запись 1-го постулата, именно : если скорость точки измерять по показаниям часов t χ , то измеренная таким способом скорость V χ, никогда не превысит скорости света . При этом истинная скорость точки V может превышать скорость света на сколько угодно. Итак, 1-й постулат появился только потому, что измеряя время реальными часами, мы полагаем, что они – идеальны. При учете материальности часов и введении формул перехода от показаний часов к истинному времени, 1-й постулат теряет силу и должен быть отменен.
1. 10. Преобразования координат
При справедливости формул сложения скоростей (1. 6) и (1. 7), нетрудно сделать вывод, что уравнения классической механики, в том числе законы сохранения импульса и энергии, остаются в классической форме, и во всех формулах должно фигурировать истинное время t . То же самое относится и к производным по времени, например:
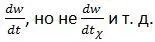
Преобразования координат есть преобразования Галилея, с добавлением формулы перехода от показаний часов к истинному времени: 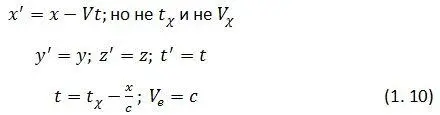
Читать дальше



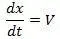 – истинная (или исправленная) скорость точки, а
– истинная (или исправленная) скорость точки, а 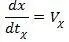 – скорость этой же точки определяемая по показаниям часов традиционным методом, без учета материальности часов. Из (1. 5) видно также, что модуль скорости V всегда больше модуля скорости V χ.
– скорость этой же точки определяемая по показаниям часов традиционным методом, без учета материальности часов. Из (1. 5) видно также, что модуль скорости V всегда больше модуля скорости V χ.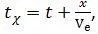 а истинное время движения равно:
а истинное время движения равно: