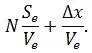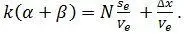Анатолий Овчинников - Рассуждения об основах физики

Далее мы будем рассматривать только прямолинейное движение материальных точек и часов вдоль оси OX . В пункте (1. 13.) мы дадим обобщение полученных результатов на трехмерное пространство.

Пусть материальная точка двигается по оси OX c некоторой скоростью V . Этот процесс можно рассматривать как преобразование пространства во время по закону x/V = t, то есть пройденному расстоянию x материальной точки ставится в соответствие некоторое время t = x/V. В частном случае, когда V = 0 можно считать, что это преобразование также имеет место, но его результат не определен.

Рассмотрим теперь часы, как и материальную точку, двигающиеся вдоль оси OX или покоящиеся. В чем сходство часов с материальной точкой? Их два. Первое – часы также материальны, как и материальная точка. Второе – часы также являются преобразователем пространства во время.

В чем отличие часов от материальной точки? Их два. Первое – часы преобразуют пространство во время, используя строго постоянную (эталонную) скорость V e по закону: t = x/V e, тогда как у материальной точки скорость, вообще говоря, может быть любой. Второе – часы, находясь в покое, сохраняют прежним результат преобразования: t = x/V e, тогда как у покоящейся материальной точки результат преобразования становится неопределенным. Таким образом, чтобы получить представление о реальных (материальных) часах, мы должны скомбинировать и сходства и различия между часами и материальной точкой (непротиворечивым образом) в одном устройстве, называемом реальными часами .

Сделав это, мы получим структурную схему часов, изображенную на рис. 1. 1.

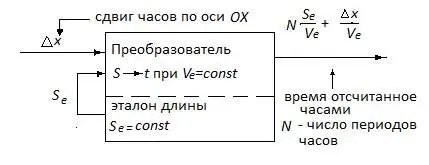
Рис. 1. 1

В преобразователе пространство – время ( s -> t ) на основе эталонной скорости V e последовательно преобразуются эталоны длины s e и часы показывают на выходе слагаемое N ( s e/V e ), где N – число периодов часов. Но если часы сдвигаются по оси OX на величину Δ x , то и эту величину преобразователь также преобразует во время (по тому же закону) равное Δ x/V e. В результате часы будут на выходе показывать сумму:

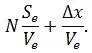
Назовем слагаемое Δ x/V e слагаемым переноса часов. Слагаемое переноса равно нулю, если во время измерений часы неподвижны. Но если допустить, что часы не материальны (но все-таки работают), то в этом случае слагаемое переноса будет равно нулю и тогда, когда часы двигаются. Истинное время, измеренное часами, равно только N ( s e/V e ) и из показаний часов следует вычитать слагаемое переноса. Чтобы придать слагаемому переноса определенный знак (– или +) договоримся о направлении эталонной скорости V e. Если часы сдвигаются независимо (от других скоростей), то будем направлять скорость V e в положительном направлении оси OX . Если же часы двигаются вместе с материальной точкой, время движения которой они измеряют, то будем направлять скорость V e также как и скорость точки V, то есть векторы v eи vодинакового направления.

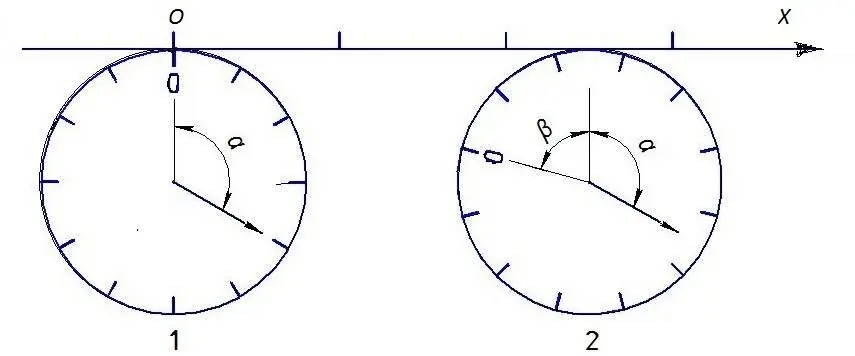
Рис. 1. 2

На рис. 1. 2 представлена наглядная механическая, одномерная модель реальных часов. Механизм часов двигается вдоль оси OX, не меняя своего направления в пространстве. Циферблат же часов, представляющий круг, может свободно вращаться вокруг своей оси и катиться по оси OX (для выполнения правила знаков он катится по оси OX снизу). Неподвижные часы (1) отсчитывают угол α пропорциональный истинному времени kα = N ( s e/V e ). Подвижные часы (2) отсчитывают угол α +β, причем β – угол поворота циферблата пропорционален слагаемому переноса, а k – коэффициент пропорциональности. Таким образом, подвижные часы отсчитают время:

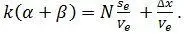
В дальнейшем договоримся показания часов снабжать индексом χ (греческое хи), то есть писать – t χ , тогда, как истинное время будем писать обычно – t и тогда:

Наиболее ясно механизм появления слагаемого переноса усматривается в световых часах. Если часы неподвижны, то путь проходимый светом за один период равен 2 s e . Но если часы двигаются вдоль оси OX (и световой импульс двигается вдоль этой же оси) то, как легко видеть, путь проходимый световым импульсом за один период будет равен не 2 s e, а равен 2 s e +Δ x, где Δ x – сдвиг часов за один период вдоль оси OX. Поэтому часы покажут время: