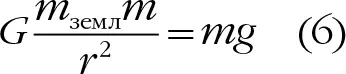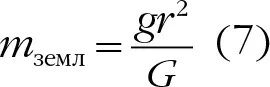Уолтер Левин - Глазами физика. От края радуги к границе времени

Поскольку относительные расстояния от Солнца до планет были известны довольно точно, знание абсолютного расстояния от Солнца до Земли с 7-процентной точностью позволяло к концу ХVII века приблизительно с такой же точностью рассчитать и абсолютные расстояния от Солнца до пяти других известных астрономам планет.

Описанный выше метод для расчета массы Солнца можно использовать и для определения массы Юпитера, Сатурна и Земли. Все три планеты имеют на своих орбитах спутники; еще в 1610 году Галилео Галилей обнаружил четыре спутника Юпитера, которые ныне известны как галилеевы луны. Если m 1 – масса Юпитера, а m 2 – масса одного из его спутников, то мы можем вычислить массу Юпитера с помощью уравнения 5 – так же, как вычисляли массу Солнца, только на этот раз r будет расстоянием между Юпитером и его спутником, а Т – орбитальным периодом этого спутника при вращении вокруг Юпитера. Четыре галилеевых луны (всего у Юпитера 63 спутника!) имеют орбитальные периоды 1,77 дня, 3,55 дня, 7,15 дня и 16,69 дня.

Со временем точность оценки расстояний между планетами и величины G существенно повысилась. К XIX веку константа G была известна с точностью до 1 процента. В настоящее время она оценена с точностью до 0,01 процента.

Приведу пример с конкретными числами. Предлагаю с помощью уравнения 5 вместе вычислить массу Земли ( m 1), взяв для этого данные об орбите нашей Луны (масса m 2). Чтобы использовать уравнение 5 правильно, расстояние r должно быть выражено в метрах, а период T в секундах. И при G, равном 6,673 × 10 −11, мы получим массу в килограммах.

Среднее расстояние от Земли до Луны ( r ) составляет 3,8440 × 10 8метров; ее орбитальный период Т равен 2,3606 × 10 6секунды (27,32 дня). Если подставить эти числа в уравнение 5, масса Земли будет равна 6,030 × 10 24килограмма. Самая точная на сегодняшний день оценка массы Земли составляет около 5,974 × 10 24килограмма, то есть всего на 1 процент меньше, чем то значение, которое мы только что рассчитали! Откуда же взялась эта разница? Одной из причин погрешности является то, что в использованном нами уравнении предполагается круговая орбита Луны, в то время как на самом деле она вытянутая, эллиптическая. В результате наименьшее расстояние до Луны составляет 363,1 тысячи километров, а наибольшее – 405,7 тысячи километров. Конечно, для законов Ньютона эллиптические орбиты не проблема, но, боюсь, сложность этих расчетов может взорвать ваш мозг. Если уже не взорвала!

Есть еще одна причина, по которой полученный нами результат массы Земли немного отличается от фактического. Дело в том, что мы основывались на предположении, что Луна вращается вокруг Земли и что Земля находится в центре ее круговой орбиты. Таким образом, в уравнениях 1 и 3 мы исходили из того, что r – это расстояние между Землей и Луной. Для уравнения 1 это верно; однако, как мы обсуждали в главе 13, на самом деле и Луна, и Земля вращаются вокруг центра масс системы Луна-Земля, расположенного примерно на 1700 километров ниже поверхности Земли. Таким образом, r в уравнении 3 чуть меньше, чем в уравнении 1.

Поскольку мы живем на Земле, у нас есть и другие способы расчета массы родной планеты. Один из них заключается в измерении гравитационного ускорения вблизи поверхности. Падая, любой объект массой m ( m может иметь любое значение) наращивает скорость с ускорением, g, то есть около 9,82 метра в секунду за секунду [29]. Средний радиус Земли приблизительно 6,371 × 10 6метра.

Теперь вернемся к уравнению 1 Ньютона. Поскольку F = ma (второй закон Ньютона), то

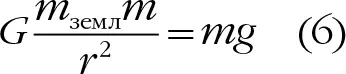
Здесь r – радиус Земли. При G = 6,673 × 10 −11, g = 9,82 метра в секунду за секунду и r = 6,371 × 10 6метра мы можем вычислить m землв килограммах (обязательно попробуйте!). Если несколько упростить уравнение 6, получаем

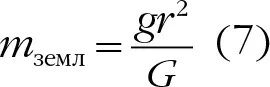
Я подсчитал, что m землсоставляет 5,973 × 10 24килограмма (впечатляет, не правда ли?).

Обратите внимание, что массы m брошенного нами объекта в уравнении 7 вообще нет! Это не должно вас удивлять, потому что масса Земли не может зависеть от массы объекта, который вы на нее роняете.

Вам, возможно, будет также интересно узнать, что, по мнению Ньютона, средняя плотность Земли составляет от 5000 до 6000 килограммов на кубический метр. Следует отметить, что эта гипотеза не основывалась на какой-либо астрономической информации; он предложил ее полностью независимо от всех своих законов. Это была наилучшая «обоснованная» прикидка великого физика. Средняя плотность Земли действительно составляет 5,540 килограмма на кубический метр. Если записать предположение Ньютона как 5,500 ± 500 килограммов на кубический метр, получится, что погрешность его оценки – всего 10 процентов (просто невероятно!).