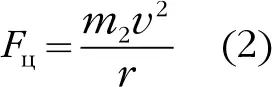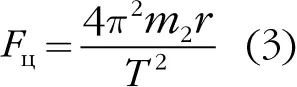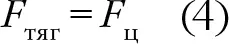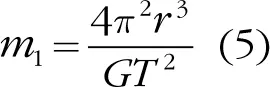Уолтер Левин - Глазами физика. От края радуги к границе времени

Если орбита круговая или почти круговая (что характерно для пяти из шести планет, известных ученым в XVII веке), темп вращения планеты на орбите будет стабильным, но направление ее скорости постоянно меняется. Однако при изменении направления скорости любого объекта, даже без изменения ее величины, непременно имеет место ускорение, и, следовательно, согласно второму закону Ньютона, должна быть сила, обеспечивающая его.

Эту силу называют центростремительной ( F ц), и она всегда направлена точно от движущейся планеты к Солнцу. Конечно, поскольку Ньютон был Ньютоном, он знал, как вычислить эту силу (я вывожу это уравнение на своих лекциях); ее величина такова:

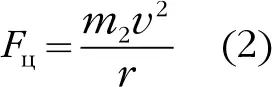
Здесь v – скорость планеты на орбите. Но эта скорость равна окружности орбиты, 2 π r, поделенной на время, T, требуемое для одного оборота вокруг Солнца. Таким образом, мы можем также записать:

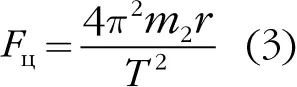
Откуда же берется эта сила? Каково ее происхождение? Ньютон понял, что это должно быть гравитационное притяжение Солнца. Следовательно, две силы в приведенных выше уравнениях являются, по сути, одной и той же силой и друг другу равны:

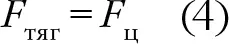
Еще немного поиграв с перестановкой переменных (кстати, отличный шанс освежить школьные знания алгебры), получаем, что масса Солнца составляет:

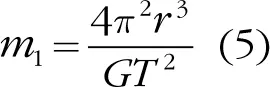
Обратите внимание, что массы планеты ( m 2) в уравнении 5 больше нет; она не входит в эту модель. Следовательно, для расчетов нам достаточно знать среднее расстояние от планеты до Солнца и ее орбитальный период ( Т ). Ну разве не удивительно? В конце концов, m 2есть и в уравнении 1, и в уравнении 2. Но именно тот факт, что данная переменная присутствует в обоих уравнениях, и является причиной, по которой m 2исключается путем установления равенства между F тяги F ц. В этом красота данного метода, и всем этим мы обязаны сэру Исааку Ньютону!

Уравнение 5 указывает на то, что r ³/ T ² одинаково для всех планет. Хотя все они находятся на совершенно разных расстояниях от Солнца и имеют разные периоды орбитального движения, соотношение r ³/ T ² у всех одинаково. Немецкий астроном и математик Иоганн Кеплер обнаружил этот удивительный факт в 1619 году, задолго до Ньютона. Но почему это отношение – куба радиуса к квадрату орбитального периода, – величина постоянная, он объяснить не смог. Только гениальный Ньютон 68 лет спустя показал, что это естественное следствие его законов.

В общем и целом уравнение 5 говорит нам о том, что если мы знаем расстояние от любой планеты до Солнца ( r ), орбитальный период этой планеты ( Т ) и гравитационную константу ( G), то мы можем вычислить массу Солнца ( m 1).

Орбитальные периоды планет с достаточно высокой степенью точности были известны ученым задолго до XVII века. Расстояния между Солнцем и планетами также были известны с высокой степенью точности задолго до XVII века, но только в относительном масштабе. Иными словами, астрономы знали, что среднее расстояние от Венеры до Солнца составляет 72,4 процента от расстояния между Землей и Солнцем, а среднее расстояние от Юпитера до Солнца в 5,2 раза больше, чем от Солнца до Земли. Но абсолютные значения этих расстояний – совершенно другая история. Например, в XVI веке, во времена великого датского астронома Тихо Браге, считалось, что расстояние от Земли до Солнца в 20 раз меньше, чем оно было на самом деле (около 150 миллионов километров). В начале ХVII века Кеплер дал более точную оценку этого расстояния, но оно по-прежнему было в семь раз меньше правильного.

Поскольку, согласно уравнению 5, масса Солнца пропорциональна кубу его расстояния (до планеты), то если расстояние r не дотягивает до реального в семь раз, масса Солнца будет меньше фактической в 7³, то есть в 343 раза – много ли проку в таких данных?

Прорыв произошел в 1672 году, когда итальянский ученый Джованни Кассини измерил расстояние от Земли до Солнца с точностью до 7 процентов (весьма внушительный по тем временам результат), а это означало, что погрешность r ³ составляла лишь около 22 процентов. Но и погрешность определения G все еще была не менее 30 процентов. Так что получается, что к концу ХVII века масса Солнца могла быть определена с точностью не выше 50 процентов.