Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

Но не противоречит ли принципу относительности аберрация? Ведь мы объясняли ее, считая, что имеется абсолютная система отсчета — неувлекаемый эфир. Однако кто сказал, что это объяснение единственно возможное?

Само по себе явление аберрации не противоречит принципу относительности.

Ему противоречит наше толкование аберрации. Ну что ж, тем хуже для объяснения.

А «сами по себе» данные эксперимента показывают только то, что возможно обнаружить.

Итак, основа — принцип относительности. В этом пункте Эйнштейн не отходит от «классики». Наоборот, он расширяет галилеевский классический принцип, расширяет границы его применения.

Беда в том, что один принцип относительности сам по себе мало проясняет положение. То, что приходится отбросить теорию неувлекаемого эфира, еще не так страшно. Мы вообще можем забыть об эфире и непредвзято исследовать опытные факты.

Но тут-то как раз и начинается непонятное.

Используем принцип относительности для анализа простого опыта.

Рассмотрим уже известные нам инерциальные системы отсчета K и K 1, относительная скорость которых равна v . Проделаем в системе K опыт по определению скорости света. Назовем его условно «опыт L ».

Для этого возьмем источник света S , неподвижный в системе K , и каким-нибудь способом (например, способом Физо) измерим скорость света. Наша экспериментальная установка неподвижна в системе K . Пусть мы получили, что скорость света равна какому-то числу c .

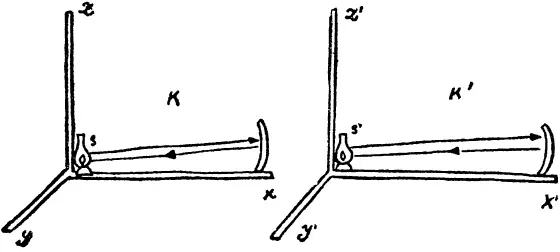
Сдублируем нашу установку в системе K 1которая движется относительно системы K так, как это показано на рисунке (возьмем источник S 1, неподвижный в системе K 1и т. д.), и проделаем аналогичный «опыт L 1». Все условия «опыта L 1» относительно системы K 1тождественно повторяют условия «опыта L » относительно системы K .

Согласно принципу относительности скорость света, измеренная в «опыте L 1», снова должна оказаться равной c , поскольку одна инерциальная система ничем не хуже другой.

Действительно, получив другое значение скорости света в системе K 1, мы убедились бы, что законы природы различны в различных инерциальных системах. Пока все хорошо.

Но мы имеем полное право рассматривать любой опыт из любой системы отсчета. Рассмотрим и опишем «опыт L 1», используя систему K .

В системе K источник света S 1и вся экспериментальная установка движутся направо со скоростью v . И мы сейчас убедимся, что в ней скорость светового луча, бегущего от этого источника направо, равна скорости света плюс скорость системы K 1относительно системы K , то есть ( c + v ). И соответственно, налево свет бежит со скоростью, равной разности скорости света и скорости системы K 1, то есть ( с – v ).

Мы подошли к очень важному месту и, чтобы лучше понять дальнейшее, перейдем от общих, абстрактных рассуждений к конкретному примеру.

Пусть физик находится со своей установкой в вагоне равномерно идущего поезда. Измерения, которые он провел, показывают, что скорость света относительно источника не зависит от направления, а постоянна и равна определенному числу — c . Иначе говоря, он установил, что свет одновременно достиг передней и задней стенок вагона через Δ t , и определил скорость

c = ½ l / Δ t .

Если вагон сделан из стекла, наблюдатель на полотне дороги также может изучать процесс распространения света. Однако для него все будет выглядеть несколько по-другому.

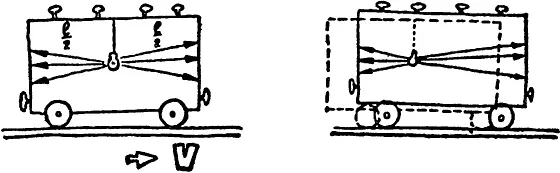
Пока свет бежит от источника к стенкам вагона, поезд проезжает некоторое расстояние. Передняя стенка «убегает», а задняя «бежит навстречу» световому лучу. До нее свет должен пройти меньшее расстояние. Но свет достигает стенок одновременно! Очевидно, это может быть только, если вперед свет распространяется с большей скоростью, чем назад.

Скорости эти можно найти совершенно просто. Как только что было сказано, скорость светового луча «вперед» равна c + v , а «назад» с – v (здесь v — скорость вагона).

Тот же самый вывод можно получить, рассуждая несколько иначе. Относительно источника света скорость света постоянна и в любой системе отсчета равна с (принцип относительности!).