Вольдемар Смилга - Очевидное? Нет, еще неизведанное…

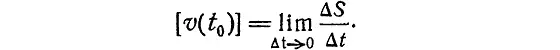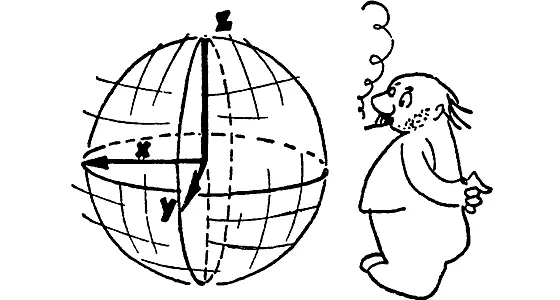
«Привязать» можно, конечно, и по-иному. Взять за центр другую точку, по-другому расположить оси и т. п.

После небольшого экскурса в математику можно более четко перефразировать определение движения.

Тело относительно данной координатной системы движется, если с течением времени изменяется хотя бы одна из его координат.

Как именно меняются координаты, показывает важнейшая характеристика движения — скорость.

Если не стремиться к строгим формулировкам (это потребовало бы несколько больше математики, чем разрешают каноны популярной литературы), то понятие скорости можно ввести так.

Пусть мы хотим определить скорость тела в какой-то момент времени t 0. Тогда нужно сделать следующее:

определить в выбранной нами системе отсчета положение тела в момент t 0. Иначе говоря, определить его координаты;

посмотреть, где окажется наше тело в какой-то следующий момент t 1(найти координаты в момент t 1);

определить длину прямолинейного отрезка, соединяющего первую и вторую точки. Эту длину обозначим Δ S ( t 1 · t 0);

поделить Δ S ( t 1 · t 0) на соответствующий интервал Δ t = ( t 1 – t 0). Тогда приближенно абсолютная величина скорости тела в момент t 0равна [ v ( t 0)] ≈ Δ S /Δ t . Чем меньше мы выберем интервал Δ t , тем точнее отношение Δ S /Δ t будет определять скорость в момент t 0.

А в пределе при t 0 → 0 наша дробь точно определяет абсолютную величину скорости тела в момент t 0. Это записывают так:

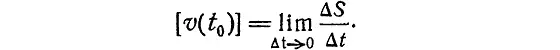
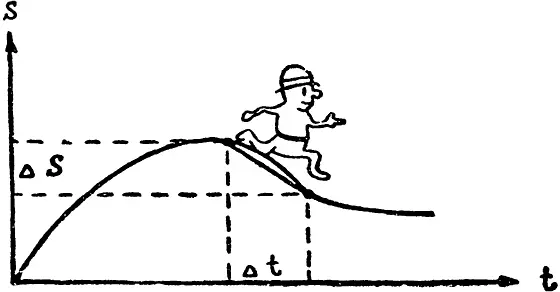
На рисунке иллюстрируются те операции, о которых только что говорилось, для частного случая, когда движение происходит вдоль прямой линии.

При этом, как видно, начиная с некоторого момента времени, S уменьшается. Это значит, что тело возвращается в начальную точку. В верхней точке кривой скорость равна нулю. Слева от этой точки скорость положительна, а справа — отрицательна. Обратите внимание, что, используя приближенное выражение для скорости, в верхней точке мы не получим нуля.

Уже упоминалось, что одной абсолютной величины еще недостаточно для полной характеристики скорости. Нужно знать направление в котором тело убегает из начальной точки.

Если тело движется не по прямой, то направление его движения изменяется весьма прихотливо, и это отражается в определении скорости. Скорость тела можно считать постоянной только тогда, когда неизменны и ее абсолютная величина и направление движения (равномерное прямолинейное движение). Очевидно, что направление скорости определяется направлением отрезка (Δ S ).

А теперь перейдем к самому важному.

Интервал пути ΔS →, как говорилось выше, определяется в данной выбранной нами системе отсчета. При этом и абсолютная величина и направление ΔS →зависят от выбора системы отсчета. В одной системе отрезок ΔS →будет один, а в другой — другой. То есть пройденный путь — величина относительная и зависит от выбора системы отсчета.

Это должно быть всем известно из школьного курса физики, поэтому ограничимся только наглядной «железнодорожной» иллюстрацией.

Путь, который проходит экспресс Москва — Ленинград в системе отсчета, жестко связанной с экспрессом, тождественно равен нулю (поезд все время находится в начале координат, и ΔS → = 0).

Если систему отсчета связать с товарным поездом, который вышел из Москвы в одно время с экспрессом, но, естественно, отставал по дороге и в момент прибытия экспресса в Ленинград находился в Бологом, то путь, пройденный экспрессом, равен расстоянию Бологое — Ленинград (ΔS → = 325 километрам).

В системе же отсчета, связанной с Землей, экспресс пройдет расстояние Москва — Ленинград, то есть ΔS → = 650 километрам. Но так как скорость определяется отношением Δ S / Δ t , то она также оказывается величиной относительной и зависит от системы отсчета.

А как интервал времени Δ t ? Он, может быть, тоже зависит от системы отсчета?

Может ли оказаться, что, определяя время движения экспресса Москва — Ленинград, мы получим в системе отсчета, связанной с Землей, один результат, а в системе, связанной с самим экспрессом, — другой? Или нелепа сама постановка такого вопроса? Надеюсь, что такой мысли ни у кого не появилось.